¿Cuáles son las aplicaciones de la derivada al análisis de funciones?

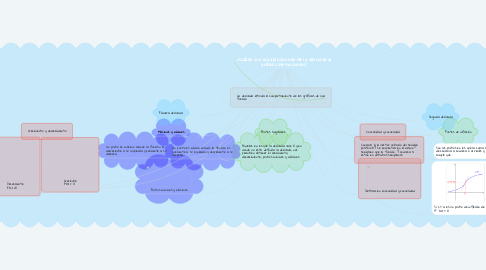
1. Puntos mínimos y máximos

2. Decreciente F'(x) <0

3. Aquellos en los que la derivada vale 0 y en donde no esta definida la derivada, nos permiten obtener el crecimiento, decrecimiento, puntos mínimos y máximos.

4. Un punto es mínimo cuando la función es creciente a su izquierda y decreciente a su derecha

5. Un punto es máximo cuando la función es decreciente a su izquierda y creciente a su derecha

6. Creciente F'(x) > 0

7. Puntos singulares

8. Máximos y mínimos

9. Crecimiento y decrecimiento

10. Primera derivada

11. La derivada estudia el comportamiento de las gráficas de una función

12. Si x = a es un punto de inflexión de f (x) ⇒ f´´(a) = 0

13. Son los puntos en los que la curva cambia de cóncava a convexa o al revés y se cumple que

14. Puntos de inflexión

15. Ilustracion concavidad y convexidad

16. Concava si el vector unitario del semieje positivo OY se encuentra en el mismo semiplano que la función. Y convexa si estan en distintos semplianos

17. Concavidad y convexidad

18. Segunda derivada