Linear System of Equations
создатель Wong Wei
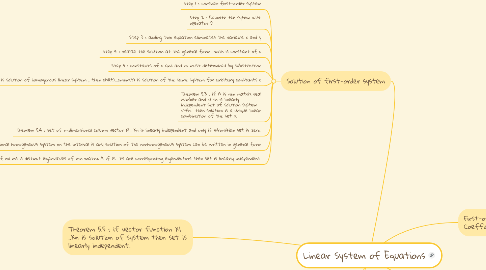

1. Theorem 5.5 : if vector function X1 ..Xn is solution of system then set is linearly independent.
2. Repeated eigenvalues
2.1. Step 1 : Subtract identity matrix multiple from original matrix A
2.2. Step 2 : Find the determinant of the matrix
2.3. Step 3 : Solve the solutions which are given by the eigenvalues
2.4. Step 4 : Combine the above solutions into the general solution
2.5. Step 5 : Calculate the values of c₁ and c₂.
2.6. Step 6 : Substitute the values of c₁ and c₂ into the general solution.
3. Solution of first-order system
3.1. Step 1 : consider first-order system
3.2. Step 2 : Rewrite the sytem with operator D
3.3. Step 3 : adding two equation eliminates the variable x and y
3.4. Step 4 : realize the solution at the general form with is constant of c
3.5. Step 5 : constants of c and and m must determined by substitution
3.6. Theorem 5.2 : x1(t)...xm(t) is solution of homogenous linear system , then c1x1(t)...cmxm(t) is solution of the same system for arbitary constants c
3.7. Theorem 5.3 : if A is nxn matrix real number and x1..xn is linearly independent set of solution system x’=Ax then solution is a unique linear combination of the set x.
3.8. Theorem 5.4 : set of n-dimensional column vector X1.. Xn is linearly independent and only if Wronskian set is zero.
3.9. Theorem 5.6 : if X1.. Xn is linearly independent then n-dimensional homogeneous system on the interval is any solution of the nonhomogeneous system can be written in general form
3.10. Theorem 5.7 : if m1..ms is distinct eigenvalues of nxn matrix A if X1 ..Xs are corresponding eigenvectors then set is linearly independent.
4. Complex Eigenvalues
4.1. Step 1 : Multiply n x n identity matrix by scalar
4.2. Step 2 : Subtract identity matrix multiple from original matrix A
4.3. Step 3 : Find the determinant of the matrix
4.4. Step 4 : Solve for the value of scalar
4.5. Step 5 : Substitute the value of scalar into the vector
4.6. Step 6 : Remove imaginary roots by rewriting using Euler's formula to get general solution
5. First-order system with Constant Coefficients
5.1. A system of linear equations of order higher than the first can be transform into a first-order system
5.2. for example, the higher order system can be transform by substitute or assume any high order variable by any new variable
6. Some Matrix Algebra
6.1. design a vector by a single symbol
6.1.1. dx/dt=X'=AX
6.2. AX=0 has nontrivial solution
6.2.1. det A=0 if X not equal to 0
6.3. 2x2 matrix multiply with matrix I equal to itself
6.3.1. IA=A , AI=A

