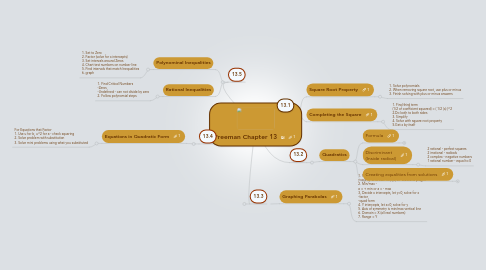
1. 13.3
1.1. Graphing Parabolas
1.1.1. 1. Find vertex - y=a(x-h)^2+k then v=(h,k) or -b/2a and plug in 2. Min/max - a = + min or a = - max 3. Decide x intercepts, let y=0, solve for x -factor -quad form 4. Y intercepts, let x=0, solve for y 5. Axis of symmetry is min/max vertical line 6. Domain = X (all real numbers) 7. Range = Y
2. 13.5
2.1. Polynominal Inequalities
2.1.1. 1. Set to Zero 2. Factor (solve for x intercepts) 3. Set intervals around Zeros 4. Chart test numbers on number line 5. Find intervals that match Inequalities 6. graph
2.2. Rational Inequalities
2.2.1. 1. Find Critical Numbers -Zeros -Undefined - can not divide by zero 2. Follow polynomial steps
3. 13.4
3.1. Equations in Quadratic Form
3.1.1. For Equations that Factor 1. Use u for b, u^2 for a - check squaring 2. Solve problem with substitution 3. Solve mini problems using what you substituted
4. 13.1
4.1. Square Root Property
4.1.1. 1. Solve polynomials 2. When removing square root, use plus or minus 3. Finish solving with plus or minus answers
4.2. Completing the Square
4.2.1. 1. Find third term (1/2 of coefficient squared) = ( 1/2 (x) )^2 2.Do both to both sides 3. Simplify 4. Solve with square root property 5.Get x by itself
5. 13.2
5.1. Quadratics
5.1.1. Formula
5.1.1.1. ax^2 +bx+c=0 Opposite of b, times the square root of, b squared minus four times a times c, divided by two times a
5.1.1.2. 1. Multiply by LCD to rid fractions 2. Plug directly into Quadratic formula 3. Solve for x 4. Check to factor out of radical
5.1.2. Discriminant (Inside radical)
5.1.2.1. 2 rational - perfect squares 2 irrational - radicals 2 complex - negative numbers 1 rational number - equal to 0
5.1.3. Creating equalities from solutions
5.1.3.1. 1. Set to x = 2. Set to zero (get everything on one side) 3. Set to factored ( )( )=0 -rid fractions with LCD 4. FOIL 5. Standard form - variables on one side of =, numbers on the other
