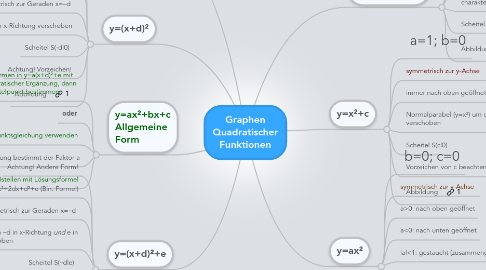
Graphen Quadratischer Funktionen by Ivo Schwalbe

Graphen Quadratischer Funktionen

y=x² Normalparabel

a=1; b=0; c=0

symmetrisch zur y-Achse

immer nach oben geöffnet

charakteristischer Punkt (1|1)

Scheitel immer S(0|0)

Abbildung

y=x²+c

a=1; b=0

symmetrisch zur y-Achse

immer nach oben geöffnet

Normalparabel (y=x²) um c in y-Richtung verschoben

Scheitel S(c|0)

Vorzeichen von c beachten

Abbildung

y=ax²

b=0; c=0

symmetrisch zur y-Achse

a>0: nach oben geöffnet

a<0: nach unten geöffnet

|a|<1: gestaucht (zusammengedrückt)

|a|>1: gestreckt (in die Länge gezogen)

a=0: Sonderfall y=0 --> Lineare Funktion auf x-Achse

Scheitel immer S(0|0)

Abbildung

y=(x+d)²

Achtung! Andere Form!

y=x²+2dx+d² (Bin. Formel)

symmetrisch zur Geraden x=–d

Normalparabel um –d in x-Richtung verschoben

Scheitel S(-d|0)

Achtung! Vorzeichen!

Abbildung

y=(x+d)²+e

Achtung! Andere Form!

y=x²+2dx+d²+e (Bin. Formel)

symmetrisch zur Geraden x=–d

Normalparabel um –d in x-Richtung *und* e in y-Richtung verschoben

Scheitel S(–d|e)

Achtung! Vorzeichen!

Achtung! In machen Lehrbüchern trifft man auch die Form y=(x-d)²+e oder y=(x-x0)²+y0 an.

Abbildung

y=ax²+bx+c Allgemeine Form

Umformen in y=a(x+d)²+e mit quadratischer Ergänzung, dann Scheitelpunkt bestimmen

oder

Scheitelpunktsgleichung verwenden

Öffnung und Krümmung bestimmt der Faktor a

Nullstellen mit Lösungsformel

Allgemeines

Graph ist "Parabel"

Kegelschnitt

Gerade

Parabel

Hyperbel

Kreis

Ellipse

...

symmetrisch zur Geraden, die vertikal durch den Scheitelpunkt verläuft

tiefster (a>0) oder höchster Punkt (a<0) ist "Scheitelpunkt"

"Anstieg" ist nicht konstant, wie bei linearer Funktion, sondern hängt von x ab

Achtung! Einem gegebenen y-Wert kann ein x, zwei x oder kein x zugeordnet sein.

Definitionsbereich: Q

Wertebereich: unterschiedlich (hängt von den Parametern ab)

Nullstellen: keine, eine oder zwei (hängt von den Parametern ab)

Scheitel aus der Funktionsgleichung ablesen oder mit Scheitelpunktsgleichung bestimmen

Nullstelle aus Funktionsgleichung ablesen oder mit Lösungsgleichung bestimmen