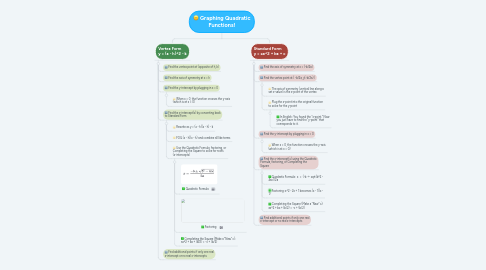
1. Vertex Form y = (x - h)^2 - k
1.1. Find the vertex point at (opposite of h, k)
1.2. Find the axis of symmetry at x = h
1.3. Find the y-intercept by plugging in x = 0
1.3.1. When x = 0, the function crosses the y-axis (which is at x = 0)
1.4. Find the x-intercept(s) by converting back to Standard Form
1.4.1. Rewrite as y = (x - h)(x - h) - k
1.4.2. FOIL (x - h)(x - h) and combine all like terms
1.4.3. Use the Quadratic Formula, factoring, or Completing the Square to solve for roots (x-intercepts)
1.4.3.1. Quadratic Formula
1.4.3.2. Factoring
1.4.3.3. Completing the Square (Make a "New" c): ax^2 + bx + (b/2) = -c + (b/2)
1.5. Find additional points if only one real x-intercept or no real x-intercepts
2. Standard Form y = ax^2 + bx + c
2.1. Find the axis of symmetry at x = (-b/2a)
2.2. Find the vertex point at ( -b/2a, y(-b/2a) )
2.2.1. The axis of symmetry (vertical line along a set x-value) is the x-point of the vertex
2.2.2. Plug the x-point into the original function to solve for the y-point
2.2.2.1. In English: You found the "x-point." Now you just have to find the "y-point" that corresponds to it.
2.3. Find the y-intercept by plugging in x = 0
2.3.1. When x = 0, the function crosses the y-axis (which is at x = 0)
2.4. Find the x-intercept(s) using the Quadratic Formula, factoring, or Completing the Square
2.4.1. Quadratic Formula: x = (-b +- sqrt(b^2 - 4ac)/2a
2.4.2. Factoring: x^2 - 2x + 1 becomes (x - 1)(x - 1)
2.4.3. Completing the Square (Make a "New" c): ax^2 + bx + (b/2) = -c + (b/2)
