Real Numbers
by Yamini Mishra
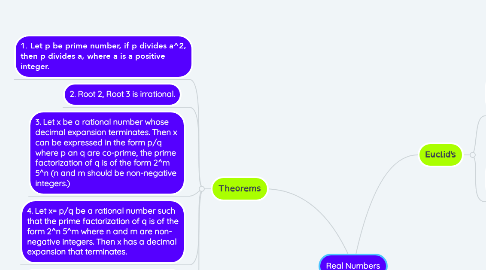

1. Theorems
1.1. 1. Let p be prime number, if p divides a^2, then p divides a, where a is a positive integer.
1.2. 2. Root 2, Root 3 is irrational.
1.3. 3. Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form p/q where p an q are co-prime, the prime factorization of q is of the form 2^m 5^n (n and m should be non-negative integers.)
1.4. 4. Let x= p/q be a rational number such that the prime factorization of q is of the form 2^n 5^m where n and m are non- negative integers. Then x has a decimal expansion that terminates.
1.5. 5. Let x= p/q be a rational number, such that the prime factorization of q is not of the form of 2^n 5^m where n and m are non- negative integers. Then x has a decimal expansion which is non-terminating repeating.
2. Prime Factorization Method
2.1. For any two positive integers a and b, HCF (a,b) × LCM (a,b) = ab.. For example- f(x)= 3x^2y; g(x)= 6xy^2. Therefore HCF= 3xy; LCM= 6x^2 y^2.
3. Euclid's
3.1. DIVISION LEMMA:- Given positive integers a and b, there exist unique integers q an r that satisfies: a= bq + r ; 0 </=r <b.
3.2. DIVISION ALGORITHM:- Steps to obtain the HCF of two positive integers say, c and d, with c > d.
3.2.1. STEP 1:- Apply Euclid's Division Lemma, to c and d. c= dq + r
3.2.2. STEP 2:- If r = zero, d is the HCF of c and d. If r is not equal to 0, apply Euclid's Division to d and r.
3.2.3. STEP 3:- Continue the process till the remainder is zero.
