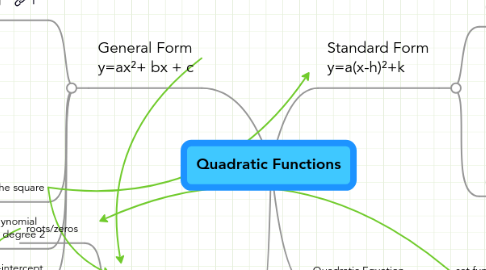
1. General Form y=ax²+ bx + c
1.1. Graphing
1.1.1. domain and range
1.1.2. transformations
1.1.2.1. changes in a (vertical stretch)
1.1.2.1.1. if a>0, the parabola opens up
1.1.2.1.2. if a<0, the parabola opens down
1.1.2.1.3. if -1<a<1 and a≠0, the parabola widens
1.1.2.1.4. if a>1 or a<-1, the parabola narrows
1.1.2.2. changes in b
1.1.2.2.1. b<0, vertex moves down and right
1.1.2.2.2. b>0, vertex moves down and left
1.1.2.3. changes in c
1.1.2.3.1. c>0, parabola moves up
1.1.2.3.2. c<0, parabola moves down
1.1.3. function
1.1.3.1. vertical line test
1.2. Completing the square
1.3. Univariate polynomial equation with degree 2
1.4. c is the y-intercept
2. Quadratic formula
2.1. roots/zeros
2.2. discriminant
2.2.1. b²-4ac
2.2.1.1. if b²-4ac=0, we have one distinct root
2.2.1.2. if b²-4ac>0, we have two dinstinct roots
2.2.1.3. if b²-4ac<0, we have two imaginary roots
3. Standard Form y=a(x-h)²+k
3.1. Graphing
3.1.1. domain and range
3.1.2. transformations
3.1.2.1. changes in a
3.1.2.2. changes in h
3.1.2.2.1. h>0, parabola shifts right
3.1.2.2.2. h<0, parabola shifts left
3.1.2.3. changes in k
3.1.2.3.1. k>0, parabola shifts up
3.1.2.3.2. k<0, parabola shifts down
3.1.3. function
3.1.3.1. Vertical line test
3.2. (h,k) = vertex
3.2.1. if a>0, vertex is the minimum
3.2.2. if a<0, vertex is the maximum
3.2.3. x=h is the axis of symmetry
