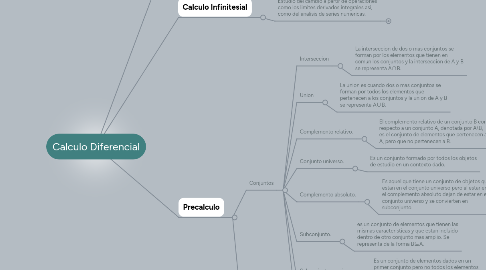
1. ¿Que son las matematemanicas?
1.1. Ciencia formal que, partiendo del ariomas y siguiendo el razonamiento logico,estudia las propiedades y relaciones entre entidades abstratas como umeros, figuras geometricas o simbolos.
1.1.1. Numeros reales(R).
1.1.1.1. Racionales(Q)
1.1.1.1.1. Enteros(Z)
1.1.1.1.2. Fraccionarios(decimales).
1.1.1.2. Irracionales.
2. Calculo Infinitesial
2.1. Estudio del cambio a partir de operaciones como los limites derivados integrales asi, como del analisis de series numericas.
2.1.1. Determine Next Stage Tasks
2.1.2. Determine Task Dependencies
2.1.3. Estimate Effort
2.1.4. Allocate Resources
2.1.5. Prepare Next Stage Schedule
2.1.6. Prepare Next Stage Budget
2.1.7. Update Project Schedule
2.1.8. Update Project Budget
2.1.9. Review Business Case
2.1.10. Review Project Organization
2.1.11. Review Project Scope
2.1.12. Prepare Stage Assessment
2.1.13. Review Stage Assessment
2.1.14. Follow-Up Stage Assessment
2.1.15. Compile Stage Closure Report
3. Precalculo
3.1. Conjuntos
3.1.1. Interseccion
3.1.1.1. La interseccion de dos o mas conjuntos se forman por los elementos que tienen en comun los conjuntos y la interseccion de A y B se representa A∩B.
3.1.2. Union
3.1.2.1. La union es cuando dos o mas conjuntos se forman por todos los elementos que pertenecen a los conjuntos y la union de A y B se representa A∪B.
3.1.3. Complemento relativo.
3.1.3.1. El complemento relativo de un conjunto B con respecto a un conjunto A, denotada por A\B, es el conjunto de elementos que pertenecen a A, pero que no pertenecen a B.
3.1.4. Conjunto universo.
3.1.4.1. Es un conjunto formado por todos los objetos de estudio en un contexto dado.
3.1.5. Complemento absoluto.
3.1.5.1. Es aquel que tiene un conjunto de objetos que estan en el conjunto universo pero al estar en el complemento absoluto dejan de estar en el conjunto universo y se convierten en subconjunto.
3.1.6. Subconjunto.
3.1.6.1. es un conjunto de elementos que tienen las mismas caracteristicas y que estan incluido dentro de otro conjunto mas amplio. Se representa de la forma B⊆A.
3.1.7. Subconjunto propio.
3.1.7.1. Es un conjunto de elementos dados en un primer conjunto pero no todos los elementos estan incluidas en el subconjunto. Se representa de la forma C⊊A.
3.1.8. Superconjunto.
3.1.8.1. Eel superconjunto es aquel que tiene la caracteristica de agrupar a otros elementos de una misma caracteristica. Se representa de la forma B⊇A.
3.2. Desigualdades o Inecuaciones.
3.2.1. Son en las que aparecen letras y números con las operaciones usuales. Las letras son las variables o incógnitas de las inecuaciones. Las inecuaciones se clasifican atendiendo al número de incógnitas y al grado de la expresión algebraica que aparece en ellas.
