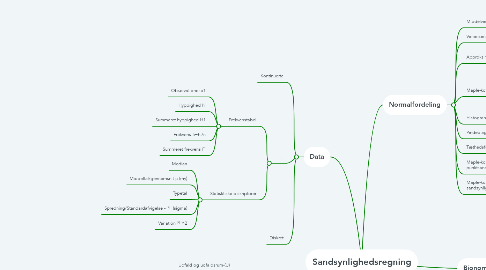
1. Data
1.1. Kontinuerte
1.2. ...
1.2.1. Frekvenstabel
1.2.1.1. Observationer x1
1.2.1.2. Hyppighed hi
1.2.1.3. Summeret hyppighed H1
1.2.1.4. Frekvens fi=hi/n
1.2.1.5. Summeret frekvens Fi
1.2.2. Statisktiske diskriptorer
1.2.2.1. Median
1.2.2.2. Middeltal/gennemsnit μ (my)
1.2.2.3. Typetal
1.2.2.4. Spredning/Standardafvigelse - 𝜎 (sigma)
1.2.2.5. Variation 𝜎^2
1.3. Diskret
2. Sandsynligheder
2.1. Udfald og udfaldsrum-(U)
2.2. Hændelser-(H) og komplementærhændelser
2.3. Komplementærhændelsen til H, er den modsatte hændelse og betegnes 𝐻 ̅
2.4. P kan betragtes som en funktion, hvor x er udfaldene, og funktionsværdierne (y-værdierne) er sandsynlighederne. Dette kaldes en sandsynlighedsfunktion
2.4.1. P(x=x)=antal gunstige udfald/antal mulige udfald
2.5. A og B er mængder
2.6. Additionsformlen
2.6.1. P(AUB=P(A)+P(B)-P(A∩B)
3. Normalfordeling
3.1. Middelværdien
3.1.1. 𝑋~𝑁(𝜇,𝜎 )
3.2. Variansen er difineret ved
3.2.1. 𝜎 ^2=n*p*(1-p)
3.3. Approksimationen
3.3.1. Jo længere sandsynligheden, p, er fra ½, jo større skal n være, for at approksimationen bliver god
3.4. Maple-kommandoer
3.4.1. Pindediagram: pindediagramBIN(n,p)
3.4.2. Graf for tæthedsfunktionen: plot(normalpdf(µ,σ,x), x = xmin .. xmax, y = ymin..ymax)
3.5. Histogram
3.6. Pindediagram
3.7. Tæthedsfunktionen
3.7.1. 𝑋~𝑁(𝜇,𝜎 )
3.8. Maple-kommando til at bestemme punktsandsynligheder
3.8.1. 𝑃(𝑋=𝑥)= binpdf(n.p.x)
3.9. Maple-kommando til at bestemme sandsynligheder af typen
3.9.1. 𝑃(𝑋≤𝑥)=bincdf(n.p.x)
4. Bionormalfordeling
4.1. Kombinatorik
4.1.1. 𝑋~𝑏(𝑛,𝑝)
4.2. Mængder
4.3. Notation
4.3.1. X: Stokastisk variabel
4.3.2. n: Antal gange forsøget udføres
4.3.3. p: Sandsynligheden for succes ved hvert forsøg
4.3.4. x: Antal gange, der er succes
4.4. Binomialkoefficienten
5. Konfidensintervaller
5.1. Et konfidensinterval er et sikkerhedsinterval, der angiver det interval omkring en værdi estimeret ud fra stikprøven, hvor den sande værdi for hele populationen formodes at befinde sig med en given sandsynlighed.
5.2. p: Den estimerede værdi (ud fra forsøget/stikprøven)
5.3. n: Antal forsøg (F.eks. antal personer i stikprøven)
5.4. 95% - Konfidensinterval
5.5. Spredning i normalfordeling
5.5.1. [𝜇-𝜎;𝜇+𝜎
