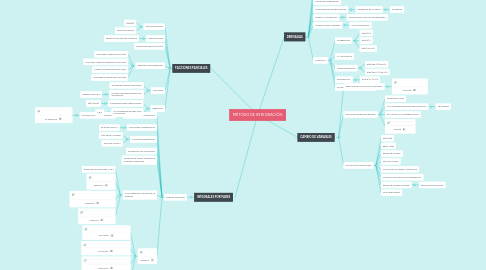
1. INTEGRALES POR PARES
1.1. PERMITE CALCULAR
1.1.1. LA INTEGRAL DE UN PRODUCTO
1.1.1.1. CON DOS FUNCIONES APLICANDO
1.1.1.1.1. LA FORMULA
1.1.2. FUNCIONES LOGARÍTMICAS
1.1.2.1. SE ELIGE COMO U
1.1.3. FUNCIÓN EXPONENCIAL
1.1.3.1. TIPO SENO- COSENO
1.1.3.2. SE ELIGE COMO V
1.1.4. SE DERIVAN LAS FUNCIONES
1.1.5. SE RESUELVE POR EL MÉTODO DE INTEGRAL INDEFINIDA
1.1.6. UNA EXPRESIÓN POR PARTES SE EXPRESA
1.1.6.1. BUENA SELECCIÓN PARA u Y du
1.1.6.2. FORMULA
1.1.6.3. FORMULA
1.1.6.4. FORMULA
1.1.7. EJEMPLO
1.1.7.1. SOLUCIÓN
1.1.7.2. SOLUCIÓN
1.1.7.3. SOLUCIÓN
1.1.7.4. RESULTADO
2. FACCIONES PARCIALES
2.1. FUNCIÓN PARCIAL
2.1.1. P(x)/Q(x)
2.1.2. FRACCIÓN PROPIA
2.2. DENOMINADOR
2.2.1. PRODUCTO DE FACTOR LINEALES
2.3. DESCOMPONER LA FACCIÓN
2.4. PERMITEN FACTORIZACIÓN
2.4.1. FACTORES LINEALES DISTINTOS
2.4.2. FACTORES LINEALES REPETIDOS O IGUALES
2.4.3. FTORES CUADRATICOS DISTINTOS
2.4.4. FACTORES CUADRÁTICOS IGUALES
2.5. DISTINTOS
2.5.1. SE FORMAN VARIAS FACCIONES
2.5.2. EL DENOMINADOR TENDRÁ UNA CONSTANTE
2.5.2.1. DETERMINAR A,B,C
2.6. REPETIDOS
2.6.1. FORMANDO VARIAS FRACCIONES
2.6.1.1. Q(x)=(ax+b)
2.6.2. EL NUMERADOR TENDRÁ UNA CONSTANTE
2.6.2.1. A,B,C
3. DERIVADAS
3.1. LIMITE QUE TIENDE A LA RAZÓN
3.1.1. APLICACIONES Y MÉTODOS
3.2. ES UNA FUNCIÓN
3.3. COCIENTE INCREMENTAL
3.4. FUNCIONES DE VALORES REALES
3.4.1. PENDIENTE DE LA RECTA
3.4.1.1. TANGENTE
3.5. TEORÍAS Y CONCEPTOS
3.5.1. ESTABLECIDOS POR LOS ANTECESORES
3.6. SE DERIVA SOLO VARIABLE
3.6.1. NO LA CONSTANTE
3.7. FORMULAS
3.7.1. ALGEBRAICAS
3.7.1.1. d/dx (c)=0
3.7.1.2. d/dx (x)=1
3.7.1.3. d/dx ( u+v-w)=
3.7.2. C= CONSTANTE
3.7.3. TRIGONOMÉTRICAS
3.7.3.1. d/dx (sen u)=(cos u) u
3.7.3.2. d/dx (cos u) =(-sen u) u
3.7.4. EXPONENCIAL
3.7.4.1. d/ dx e^n= (e^n) u
3.7.5. SE DIFERENCIA ENTRE LOS 2 TÉRMINOS
4. CAMBIO DE VARIABLES
4.1. DERIVADA DE LA FUNCIÓN COMPUESTA
4.1.1. FUNCIÓN
4.2. PASOS DE CAMBIO DE VARIABLE
4.2.1. SE DESPEJA u y dx
4.2.2. SI LA INTEGRAR RESULTANTE ES SENCILLA
4.2.2.1. SE INTEGRA
4.2.3. SE VUELVE A LA VARIABLE INICIAL
4.2.4. Función
4.3. SUSTITUCIÓN HACIA ATRÁS
4.3.1. d/dx g (fx)
4.3.2. dg/df . df/dx
4.3.3. REGLA DE CADENA
4.3.4. DOMINIO CLARO
4.3.5. CALCULAR LA INTEGRAL INDEFINIDA
4.3.6. SUMAR LA CONSTANTE DE INTEGRACIÓN
4.3.7. REGLA DE CADENA INVERSA
4.3.7.1. REGLA DE SUSTITUCIÓN
4.3.8. SE DIVIDE ENTRE 3
