1. Tipos de conjuntos
1.1. Conjunto Unitario
1.2. Conjunto finito
1.3. Conjunto Infinito
1.4. Subconjuntos
1.5. Conjunto universal
1.6. Conjunto vacío
1.7. Conjunto potencia
1.8. Subconjunto propio
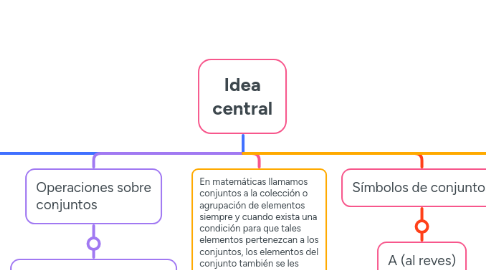
2. Operaciones sobre conjuntos
2.1. Son operaciones que se hacen sobre conjuntos
3. En matemáticas llamamos conjuntos a la colección o agrupación de elementos siempre y cuando exista una condición para que tales elementos pertenezcan a los conjuntos, los elementos del conjunto también se les denomina objetos del conjunto.
4. Símbolos de conjuntos
4.1. A (al reves)
5. Propiedades de conjuntos
5.1. Conmutativa
5.1.1. Esta propiedad nos dice que el resultado de una operación es el mismo cualquiera que sea el orden de los elementos con los que operan. Unión A U B = B U A Intersección: A ∩ B = B ∩ A
5.2. Asociativa
5.2.1. Nos dice que el resultado de una operación, en la que intervienen 3 o mas números, es independiente del agrupamiento de los números. Unión: A U (B U C)=(A U B) U C Intersección: A ∩ (B ∩ C)=(A ∩ B) ∩ C
5.3. Distributiva
5.3.1. Los términos de una operación de unión o intersección de varios conjuntos pueden agruparse de forma indistinta, obteniendo siempre el mismo resultado. Unión: A U (B ∩ C)= (AUB) ∩ (A U C) Intersección: A ∩ (B U C)= (A∩B) U (A∩C)
5.4. Ley de Morgan
5.4.1. El complemento de la unión de dos conjuntos es igual a la intersección de sus complementos, y el complemento de la intersección de dos conjuntos es igual a la unión de sus complementos. Unión: (A U B U C)’= A’∩ B’ ∩ C’ Intersección: (A ∩ B ∩ C)’= A’ U B’ U C’
5.5. Propiedad de diferencia
5.5.1. La diferencia de un conjunto respecto a otro es igual a la intersección del primero con el complemento del segundo. (A – B) = A ∩ B’
5.6. Propiedad de identidad
5.6.1. Se da cuando dos objetos que aparentemente son distintos por la forma en la que se representan, al final son lo mismo. Por lo tanto, una identidad es una igualdad entre dos expresiones, entre los conjuntos existen una serie de leyes de identidades A ∪ ∅ = A "la unión de un conjunto cualquiera con el conjunto vacío es el mismo conjunto". A ∩ U = A "la intersección de un conjunto cualquiera con el conjunto universal es el mismo conjunto".
