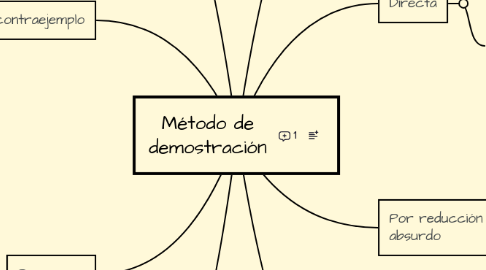
Método de demostración
por Midori Honda

1. Progresivo regresivo
1.1. Partiendo de la hipótesis se llega a la conclusión. O partiendo de la conclusión se llega a la hipótesis.
2. Directa
2.1. Partiendo de las hipótesis se avanza progresivamente hacia la conclusion, a partir de sólo afirmaciones verdaderas
3. Por reducción al absurdo
3.1. Suponiendo que la conclusion es falsa, realizamos el proceso de demostración y llegaremos a un punto de contradicción (!) que implica que la proposición debe ser cierta
4. Inducción Matemática
4.1. Para propiedades de los numeros naturales: se prueba para la función evaluada en "uno", se asume para la función evaluada en "ene" y si se demuestrar que es cierto para "ene más uno", queda demostrado.
4.1.1. Definición: Sea n∈Z tal que n≥0. Definimos el factorial de n, denotado por n!, como sigue: i) 0! = 1; ii) n!= (n-1)!n ∀ n≥1 Proposición 1: Si n≥1, entonces n!=n (n-1)∙∙∙2 ∙1 Demostración: Si n=1, entonces el miembro derecho de la igualdad se reduce a un solo factor, que es la unidad, mientras que 1!=0! ∙1=1 ∙1=1 Sea n>1 y continuamos la demostración por inducción. Se tiene (n-1)!=(n-1)∙(n-2)∙∙∙2 ∙1, de donde n!=(n-1)!n=n∙(n-1)∙∙∙2∙1 lo que termina la demostración. (Cárdenas, Lluis, Raggi & Tomás, 1973)
5. Por contraejemplo
5.1. Para demostrar que una proposición es falsa, buscamos valores con los que la proposición no se cumpla.
5.1.1. P.D.
6. Por casos
6.1. Cuando la hipótesis se puede partir en dos o más secciones, demostramos por cualquier método que cada una de estas secciones de la hípótesis implica la conclusion, y por lo tanto queda demostrado.
6.1.1. P.D.

