Многогранники

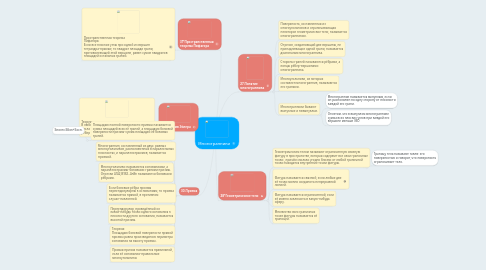
1. 29*Теоремв Эйлера

1.1. Теорема: В любом выпуклом многограннике сумма числа граней и числа вершин больше числа рёбер на 2.

2. 30.Призма

2.1. Площадью полной поверхности призмы называется сумма площадей всех её граней, а площадью боковой поверхности призмы-сумма площадей её боковых граней.

2.1.1. Sполн=Sбок+Sосн.

2.2. Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и параллелограммов, называется призмой.

2.3. Многоугольники называются основаниями, а параллелограммы-боковыми гранями призмы. Отрезки А1А2,В1В2...АnBn называются боковыми рёбрами.

2.4. Если боковые рёбра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае-наклонной.

2.5. Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

2.6. Теорема: Площадью боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

2.7. Прямая призма называется правильной, если её основания-правильные многоугольники.

3. 31*Пространственная теорема Пифагора

3.1. Пространственная теорема Пифагора: Если все плоские углы при одной из вершин тетраэдра-прямые, то квадрат площади грани, противолежащей этой вершине, равен сумме квадратов площадей остальных граней.

4. 27.Понятие многогранника

4.1. Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником.

4.2. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

4.3. Стороны граней называются рёбрами, а концы рёбер-вершинами многогранника.

4.4. Многоугольники, из которых составлен многогранник, называются его гранями.

4.5. Многогранники бывают выпуклые и невыпуклые.

4.5.1. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

4.5.2. Отметим. что в выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360

5. 28*Геометрическое тело

5.1. Геометрическим телом называют ограниченную связную фигуру в пространстве, которая содержит все свои граничные точки , причём сколько угодно близко от любой граничной точки находятся внутренние точки фигуры.

5.1.1. Границу тела называют также его поверхностью и говорят, что поверхность ограничивает тело.

5.2. Фигура называется связной, если любые две её точки можно соединить непрерывной линией.

5.3. Фигура называется ограниченной, если её можно заключить в какую-нибудь сферу.

5.4. Множество всех граничных точек фигуры называется её границей.