Problem Solving
Danielle Pにより
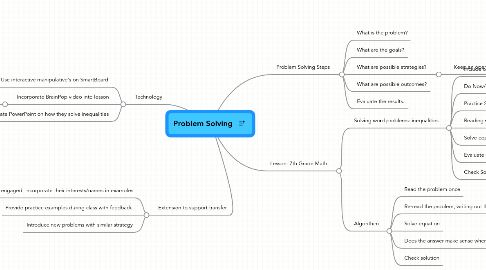

1. Technology
1.1. Use interactive manipulative's on SmartBoard
1.2. Incorporate BrainPop video into lesson
1.2.1. http://www.brainpop.com/math/algebra/solvinginequalities/index.weml
1.3. Have students work in pairs to create PowerPoint on how they solve inequalities
1.3.1. *Also provides assessment
2. Extension to support transfer
2.1. Keep students engaged, incorporate their interests/names in examples
2.2. Provide practice examples during class with feedback
2.3. Introduce new problems with similar strategy
3. Problem Solving Steps
3.1. What is the problem?
3.2. What are the goals?
3.3. What are possible strategies?
3.3.1. Keep an open mind for different possibilities!
3.4. What are possible outcomes?
3.5. Evaluate the results.
4. Lesson: 7th Grade Math
4.1. Solving word problems: inequalities
4.1.1. Include objective/aim of lesson
4.1.2. Do Now/Prior Knowledge: include examples of writing out inequalities
4.1.3. Practice Solving inequalities
4.1.4. Reading word problem, one sentence at a time, write out mathematical statements into an solvable equation
4.1.5. Solve equation
4.1.6. Evaluate the answer. Ask yourself, Does my answer make sense?
4.1.7. Check Solution
4.2. Algorithim
4.2.1. Read the problem once
4.2.2. Re-read the problem, writing out the information into a solvable equation
4.2.3. Solve equation
4.2.4. Does the answer make sense when you re-read the problem?
4.2.5. Check solution
