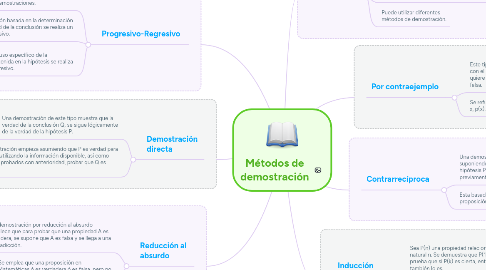
Métodos de demostración
von Diana Esparza
1. Progresivo-Regresivo
1.1. Técnica fundamental para hacer demostraciones.
1.2. La demostración basada en la determinación de la veracidad de la conclusión se realiza un proceso regresivo.
1.2.1. Proceso regresivo se inicia preguntando ¿cómo o cuando puedo concluir que la conclusión es verdadera? denominada pregunta de abstracción.
1.3. Cuando se hace uso específico de la información contenida en la hipótesis se realiza un proceso progresivo.
1.3.1. El proceso progresivo se inicia con la hipótesis, que se supone es verdadera, y se obtiene a partir de ella otra hipótesis, la cual se sabe que es verdadera ya que la primera es verdadera.
2. Demostración directa
2.1. Una demostración de este tipo muestra que la verdad de la conclusión Q, se sigue lógicamente de la verdad de la hipótesis P.
2.2. La demostración empieza asumiendo que P es verdad para después, utilizando la información disponible, así como teoremas probados con anterioridad, probar que Q es verdad.
3. Reducción al absurdo
3.1. Una demostración por reducción al absurdo establece que para probar que una propiedad A es verdadera, se supone que A es falsa y se llega a una contradicción.
3.2. Se emplea que una proposición en Matemáticas ó es verdadera ó es falsa, pero no ambas cosas a la vez.
4. Inducción matemática
4.1. Sea P(n) una propiedad relacionada con el número natural n. Se demuestra que P(1) es cierta. Se prueba que si P(k) es cierta, entonces P(k+1) también lo es.
4.2. En ese caso, la propiedad P(n) es válida para cualquier n Є N.
5. Por contraejemplo
5.1. Este tipo de demostración, íntimamente relacionada con el cuantificador universal, aparece cuando se quiere probar que una proposición del tipo x, p(x) es falsa.
5.2. Se refuta la proposición x, p(x).
6. Por casos
6.1. Utiliza las reglas de inferencia.
6.2. Se basa en demostrar que p → q es correcta, donde p es la fórmula p1 ˅ p2˅ … ˅ pn, se debe demostrar que cada una de las deducciones p1 → q, p2 → q, …, pn → q se cumplan.
6.3. Puede utilizar diferentes métodos de demostración.
7. Contrarrecíproca
7.1. Una demostración es por la contrarrecíproca cuando suponiendo que la conclusión Q, es falsa y utilizando la hipótesis P y otros teoremas y equivalencias lógicas establecidas previamente, se concluye que P es falso.
7.2. Esta basada en la equivalencia lógica entre una proposición condicional y su contrarrecíproca, P −> Q <-> ¬Q −> ¬P


