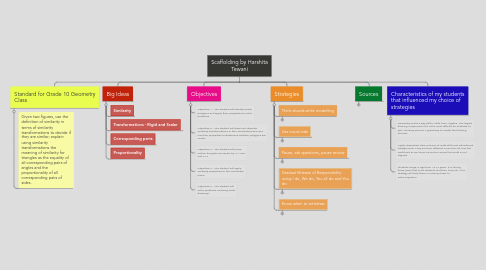
1. Standard for Grade 10 Geometry Class
1.1. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.
2. Big Ideas
2.1. Similarity
2.2. Transformations - Rigid and Scalar
2.3. Corresponding parts
2.4. Proportionality
3. Objectives
3.1. Objective 1 - The student will identify similar polygons and apply their properties to solve problems.
3.2. Objective 2 - The student will draw and describe similarity transformations in the coordinate plane and use their properties to determine whether polygons are similar.
3.3. Objective 3 - The student will prove certain triangles are similar by AA, SSS, and SAS
3.4. Objective 4 - The student will apply similarity properties to the coordinate plane
3.5. Objective 5 - The student will solve problems involving scale drawings.
4. Strategies
4.1. Think alouds while modelling
4.1.1. I think this is by far my most effective strategy. I use it in combination with working backwards. For example, I like to say this is what the question is asking me to find. What do I need in order to find what I need? What do I have? Is there a way to get from what I have to what I need? As I work through the problem, the students see how I apply what I have.
4.2. Use visual aids
4.2.1. This is specially useful for word problems in Math. Most students get thrown off by the winding problems. Sometimes, visually segregating all information into parts helps students break down the problem into understandable parts
4.3. Pause, ask questions, pause review
4.3.1. All students are different. It is hard to say that the pace that worked, for a particular topic, the previous year would work fine this year as well. It is very important to check for understanding at each step. Sometimes the only way to go fast is to go slow. On the other hand, sometimes, if the understanding is crystal clear, the teacher may swiftly move through the basics and take the students to a higher level of thinking in a very little time.
4.4. Gradual Release of Responsibility using I do, We do, You all do and You do
4.4.1. This is how one of my teacher taught math and I know I benefited immensely from it. Not to say that this is the only way but this is a great way to do formative assessment along the way. A teacher need not demonstrate to every student each and every kind of problem. The first few problems teach students how to think and then they take it from there. The art of scaffolding lies in the teacher withdrawing support at the right time. Using differentiation, after the initial steps, a teacher can divide the class into groups and provide various degrees of support. At the end of the day, there will always be some students who need to be demonstrated everything that you want them to know.
4.5. Know when to withdraw
4.5.1. Because of the diversity in my class, it is important to know when to stop providing support and encourage student thinking.
