Learning Mathematics

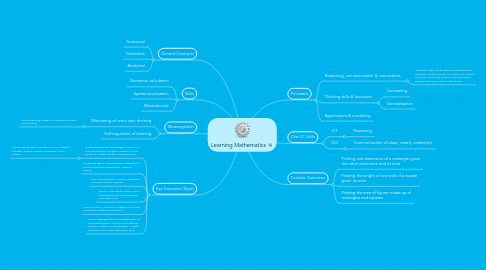
1. General Concepts

1.1. Numerical

1.2. Geometric

1.3. Analytical

2. Skills

2.1. Numerical calculation

2.2. Spatial visualisation

2.3. Measurement

3. Metacognition

3.1. Monitoring of one's own thinking

3.1.1. Active learning: Students to think about their own thinking

3.2. Self-regulation of learning

4. Key Concepts (Topic)

4.1. Students have prior knowledge of area in P3. They are able to count the number of units square to understand the concept of area.

4.1.1. Square, Rectangles, Formula of Area = length x breadth, Regular shapes, Properties of the shapes

4.2. Composite figure of squares and rectangles (In P3, they see them individually), Irregular shapes

4.3. Key concept of area: surface area that it occupies without overlaps

4.4. How to make sense of the units of measurement of area like square centimeters, etc

4.5. Misconception: Confusion between perimeter and area (in relation to formula)

4.6. Issues: Strategies to find area/perimeter of composite figures. Not the most efficient method. Problem in visualization - unable to partition the composite figure at all

5. Processes

5.1. Reasoning, communication & connections

5.1.1. Students might not be able to understand the concepts via the formula. (Too abstract) Can we hear their reasoning of their thinking or even reasons why they made certain errors?

5.2. Thinking skills & heuristics

5.2.1. Comparing

5.2.2. Generalisation

5.3. Applications & modelling

6. 21st CC Skills

6.1. CIT

6.1.1. Reasoning

6.2. CCI

6.2.1. Communication of ideas, clearly, coherently

7. Content Outcomes

7.1. Finding one dimension of a rectangle given the other dimension and its area

7.2. Finding the length of one side of a square given its area

7.3. Finding the area of figures made up of rectangles and squares