Funciones Logarítmicas y exponenciales

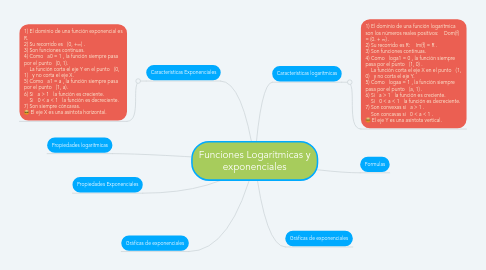
1. Propiedades logarítmicas

2. Propiedades Exponenciales

3. Gráficas de exponenciales

4. Características Exponenciales

4.1. 1) El dominio de una función exponencial es R. 2) Su recorrido es (0, +∞) . 3) Son funciones continuas. 4) Como a0 = 1 , la función siempre pasa por el punto (0, 1). La función corta el eje Y en el punto (0, 1) y no corta el eje X. 5) Como a1 = a , la función siempre pasa por el punto (1, a). 6) Si a > 1 la función es creciente. Si 0 < a < 1 la función es decreciente. 7) Son siempre cóncavas. 8) El eje X es una asíntota horizontal.

5. Características logaritmicas

5.1. 1) El dominio de una función logarítmica son los números reales positivos: Dom(f) = (0. + ∞) . 2) Su recorrido es R: Im(f) = R . 3) Son funciones continuas. 4) Como loga1 = 0 , la función siempre pasa por el punto (1, 0) . La función corta el eje X en el punto (1, 0) y no corta el eje Y. 5) Como logaa = 1 , la función siempre pasa por el punto (a, 1) . 6) Si a > 1 la función es creciente. Si 0 < a < 1 la función es decreciente. 7) Son convexas si a > 1 . Son concavas si 0 < a < 1 . 8) El eje Y es una asíntota vertical.

6. Gráficas de exponenciales

7. Formulas