1. Properties of addition
1.1. Closure property
1.1.1. Any two integers a and b, the sum (a+b) is also an integer.
1.1.1.1. 5 + 4 = 9
1.2. Commutative property
1.2.1. Any two integers a and b, the sum a + b = b + a.
1.2.1.1. -10 + 2 = 2 + -10
1.3. Associative property
1.3.1. Any three integers a, b and c, (a + b) + c = a + (b + c)
1.3.1.1. (6 + 8) + 10 = 6 + (8 + 10)
1.4. Additive Identity
1.4.1. for any integer a, a + 0 = a
1.4.1.1. 5 + 0 = 5
1.5. Additive inverse
1.5.1. For any integer a, there exists an integer -a such that a + (-a) = 0
1.5.1.1. 20 + (-20) = 0
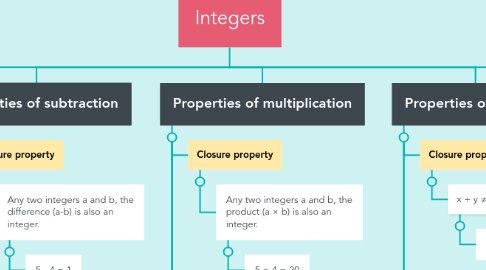
2. Properties of subtraction
2.1. Closure property
2.1.1. Any two integers a and b, the difference (a-b) is also an integer.
2.1.1.1. 5 - 4 = 1
2.2. Commutative property
2.2.1. Any two integers a and b, the difference a - b ≠ b - a.
2.2.1.1. -10 - 2 ≠ 2 - (-10)
2.3. Associative property
2.3.1. Any three integers a, b and c, (a - b) - c ≠ a - (b - c)
2.3.1.1. (6 - 8) - 10 ≠ 6 - (8 - 10)
2.4. Identity property
2.4.1. any integer a, a - 0 ≠ 0 - a
2.4.1.1. -5 - 0 = -5
3. Properties of multiplication
3.1. Closure property
3.1.1. Any two integers a and b, the product (a × b) is also an integer.
3.1.1.1. 5 × 4 = 20
3.2. Commutative property
3.2.1. Any two integers a and b, the product a × b = b × a.
3.2.1.1. -10 × 2 = 2 × -10
3.3. Associative property
3.3.1. Any three integers a, b and c, (a × b) × c = a × (b × c)
3.3.1.1. (6 × 8) × 10 = 6 × (8 + 10)
3.4. Identity property
3.4.1. any integer a, a × 1 = 1 × a = a
3.4.1.1. -10 × 1 = -10
4. Properties of Division
4.1. Closure property
4.1.1. x ÷ y ≠ Z
4.1.1.1. 5 ÷ 4 ≠ 20
4.2. Commutative property
4.2.1. x ÷ y ≠ y ÷ x
4.2.1.1. -10 ÷ 2 ≠ 2 ÷ -10
4.3. Associative property
4.3.1. (x ÷ y) ÷ z ≠ x ÷ (y ÷ z)
4.3.1.1. (6 ÷ 8) ÷ 10 ≠ 6 ÷ (8 ÷ 10)
5. Distrubutive property
5.1. Distributivity of multiplication over addition holds true for integers
5.1.1. For any integers a, b and c, a × (b + c) = (a × b) + (a × c)
5.1.1.1. 6 × (8 + 10) = (6 × 8) + (6 × 10)
5.1.1.2. Distributivity of multiplication over substraction holds true for integers
5.1.1.2.1. For any integers a, b and c, a × (b - c) = (a × b) - (a × c)
