1. Решение (частное решение) Д.у. y(0)=y(x(0))
2. Интеграл решения (общее решение) Д.у. f(x;y)=0
2.1. интегральная кривая
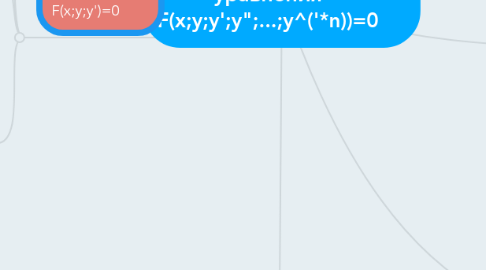
3. I-ого порядка F(x;y;y')=0
3.1. решение задача Коши (поиск функции которая пройдёт через (x(0);y(0))
3.2. y=ф(x;c)
3.2.1. при любом "С" должно быть решением
3.2.2. при y(x(0))=y(0), найдётся такое С(0), что y=ф(x;c(0)) удовлетворяет условиям y(0)=ф(x(0);c(0))
3.3. особые решения (решения, которые не получаются из общего решения)
3.4. с разделяющимися переменными
3.4.1. P(x)dx+Q(y)dy=0
3.4.1.1. ∫P(x)dx+∫Q(y)dy=C
3.4.2. P1(x)*Q1(y)dx+P2(x)*Q2(y)dx=0
3.4.2.1. ∫(P1/P2)dx+∫(Q2/Q1)dy=C
3.4.3. y'=f(x)*g(y)
3.4.3.1. ∫(1/g)dy=∫fdx+C
4. Линейные n-ого порядка y^('*n)+P1(x)y^('*(n-1))+...+P(n-1)(x)y"+Pn(x)y=f(x)
4.1. однородные (ЛОДУ) при f(x)=0
4.2. неоднородные (ЛНДУ) при f(x)≠0
4.3. I-ого порядка y'+P(x)y=Q(x)
4.3.1. метод Бернули
4.3.1.1. u'v+u(v'+P(x)v)=Q(x)
4.3.1.1.1. 1. u'+P(x)v=0 при С=0
4.3.1.1.2. 2. u'v=Q(x)
4.3.2. метод вариации произвольной постоянной
4.3.2.1. выражаем "y"
4.3.2.1.1. берём производную от "y"
4.4. II-ого порядка y"+P(x)y'+Q(x)y=f(x)
4.4.1. линейно однородные (ЛОДУ II), где f(x)=0 в области (a;b)
4.4.1.1. свойства
4.4.1.1.1. если y1(x)-решение, то y=C*y1(x) тоже решение
4.4.1.1.2. если y1(x), y2(x)-решение, то y=y1(x)+y2(x) тоже решение
4.4.1.1.3. если y1(x), y2(x)-решение, то y=C1*y1(x)+C2*y2(x) тоже решение
4.4.1.1.4. если ф1(x),ф2(x)-решение ЛНДУ II, то y=ф1(x)-ф2(x) решение ЛОДУ II
4.4.1.2. y1(x) и y2(x) - линейно независимые решения, то
4.4.1.2.1. y=C1y1(x)+C2y2(x)
4.4.1.3. с постоянными коэффициентами y"+py'+qy=0(формула Эйлера)
4.4.1.3.1. y"=k^2, y'=k, y=1
4.4.2. линейно НЕоднородные (ЛНДУ II), где f(x)≠0 в области (a;b)
4.4.2.1. Y=Yоб+Yчн
4.4.2.1.1. Yчн=ф(x) -частное решение ЛНДУ II
4.4.2.2. с постоянными коэффициентам y"+py'+qy=f(x)
4.4.2.2.1. Y=Yоб+Yчн
5. уравнение Бернули y'+P(x)y=Q(x)y^a где а≠0 и а≠1
5.1. при а>0, то y≡0
6. dd
7. Определитель Вронского Wy1y2(x)=матрица: y1(x),y2(x)-первая строчка y'1(x),y'2(x)-вторая строчка
8. Функции y1(x) и y2(x) в области (a;b)
8.1. Линейно независимые функции y1(x)/y2(x)≠const в области (a;b)
8.2. Линейно зависимые y1(x)/y2(x)=const, следовательно y1(x)=λy2(x), где λ-некоторое число не равное нулю
9. однородные P(x;y)dx+Q(x;y)dy=0, где P и Q одного порядка
9.1. I-ого порядка y'=f(x;y), где f(x;y)-однородная функция 0-ого порядка
10. с интегрируемым множителем P(x;y)dx+Q(x;y)dy=0, где ∂P/∂y≠∂Q/∂x
10.1. функция μ(x;y) называется интегрирующим множителем для Д.У.
10.1.1. при Q≠0, [∂P/∂y-∂Q/∂x]/Q=k(x)
10.1.1.1. тогда μ(x)=e^(∫k(x)dx)
10.1.1.1.1. μ=μ(x) т.к. ∂μ/∂y=0
10.1.2. при P≠0, [∂Q/∂x-∂P/∂y]/P=m(y)
10.1.2.1. тогда μ(y)=e^(∫m(y)dy)
10.1.2.1.1. μ=μ(y) т.к. ∂μ/∂x=0
10.2. μPdx+μQdy=0, где ∂(μP)/∂y=∂(μQ)/∂x
11. в полных дифференциалах P(x;y)dx+Q(x;y)dy=0, где dU(x;y)=P(x;y)dx+Q(x;y)dy
11.1. функция U(x;y) называется потенциальной функцией
11.2. U(x;y)=C
11.3. ∂P/∂y=∂Q/∂x
11.3.1. dU=(∂U/∂x)dx+(∂U/∂y)dy
11.3.1.1. ∂U/∂x=P(x;y)
11.3.1.2. ∂U/∂y=Q(x;y)
11.3.2. U=∫Pdx+ф(y)
11.3.2.1. ∂U/∂y=∂(∫Pdx)/∂y+ф'(y)
11.3.2.1.1. ф'(y)=[Q-∂(∫Pdx)/∂y=f(y)]
12. II-ого порядка F(x;y;y';y")=0
12.1. y=ф(x;C1;C2)
12.1.1. при любых значениях С1, С2 является решением
12.1.2. при любых начальных условиях найдутся такие значения С1=С10, С2=С20, что функция y=ф(x;C10;C20) удовлетворяет y(0)=ф(x(0);C10;C20)
12.2. решение задачи Коши (начальные условия) y(x(0))=Y(0) y'(x(0))=y1
12.3. допускающие понижение порядка
12.3.1. F(x;y")=0
12.3.1.1. y"=f(x)
12.3.1.1.1. y'=∫f(x)dx+C1
12.3.2. F(x;y';y")=0
12.3.3. F(y;y';y")=0
12.3.3.1. y'=P(y), y"=P*dP/dy=P*P'
12.3.3.1.1. F(y;P;P')=0
