Решение квадратного уравнения

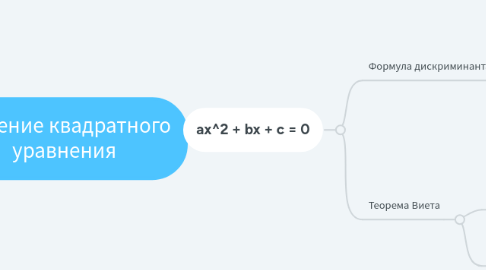
1. ax^2 + bx + c = 0

1.1. Формула дискриминанта: D = b^2 - 4ac

1.1.1. Если D > 0, то уравнение имеет два различных вещественных корня.

1.1.1.1. Находим х1 и х2

1.1.1.1.1. x1=(-b+корень(b^2-4ac))/2a

1.1.1.1.2. x2=(-b-rjhtym(b^2-4ac))/2a

1.1.2. Если D = 0, то оба корня вещественны и равны.

1.1.2.1. Находим х1 и х2

1.1.2.1.1. x1=x2=(-b+корень(b^2-4ac))/2a

1.1.3. Если D < 0, то оба корня являются комплексными числами.

1.1.3.1. Нет решений

1.1.3.1.1. Ответ

1.2. Теорема Виета

1.2.1. В случае неприведенного квадратного уравнения ax^2 + bx + c = 0: x1 + x2 = -b / a x1*x2 = c / a

1.2.1.1. Находим х1 и х2

1.2.1.1.1. Ответ

1.2.2. В случае приведенного квадратного уравнения: x1 + x2 = -p x1*x2 = q

1.2.2.1. Находим х1 и х2

1.2.2.1.1. Ответ