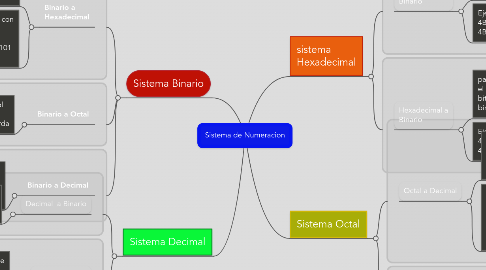
1. Sistema Binario
1.1. Binario a Hexadecimal
1.1.1. se realiza teniendo en cuenta la tabla de equivalencias entre los sistemas y por eso por dada numero hexadecimal el equivalente binario son de 4 bits se agrupan de 4 en 4 y se empieza por el numero mas significativo
1.1.2. Para esta conversión se agrupa los bits de cuatro comenzando con los primeros 4 bits de la izquierda de la derecha. Ejemplos 011011010101 = 0110 1101 0101 (0110 = 4) (1101 = 13 = D) (0101 = 5) resultado 0110 1101 0101 = 4D5
1.2. Binario a Octal
1.2.1. se agrupan la cantidad de 3 en 3 iniciando el lado derecho si al terminar de agrupar no completa 3 digitos rellenar con 0 a la izquierda
1.3. Binario a Decimal
1.3.1. se debe iniciar por el lado derecho del numero binario, cada cifra multiplicarla por 2 elevado a la potenciaconsecutiva posterior a la multiplicación hecha, se suman todos y el numero resultante era equivalente al sistema decimal.
2. Sistema Decimal
2.1. Decimal a Binario
2.1.1. Para convertir un número de sistema decimal a binario debemos dividir este número entre 2, hasta que el dividendo sea menor a 2, es decir 1.
2.2. Decimal a octal
2.2.1. Para convertir un número en base decimal a base octal se divide dicho número entre 8, luego los restos de las divisiones leídos en orden inverso indican el número en octal
3. sistema Hexadecimal
3.1. Hexadecimal a Binario
3.1.1. para pasar de Hexadecimal a binario, se remplaza el número Hexadecimal por el equivalente de 4 bits, de forma similar a como se hace de octal a binario
3.1.2. Ejemplos 4B2 = 4 11 2 4 = 0100 11 = 1011 2 = 0010 4B2 = 0100 1011 0010
3.2. Hexadecimal a Binario
3.2.1. para pasar de Hexadecimal a binario, se remplaza el número Hexadecimal por el equivalente de 4 bits, de forma similar a como se hace de octal a binario
3.2.2. Ejemplos 4B2 = 4 11 2 4 = 0100 11 = 1011 2 = 0010 4B2 = 0100 1011 0010
4. Sistema Octal
4.1. Octal a Decimal
4.1.1. En esta caso basta usar el mismo método de conversión con los números binarios. Pero en vez de hacer divisiones sucesivas entre 2 hay que efectuarlas entre 8. Nótese que el divisor corresponde a la base del sistema al cual se va a convertir.
4.1.2. Ejemplos 125 (Octal) 125/8 = 15 Residuo = 5 15/8 = 1 Residuo = 7 1/8 = 0 Residuo = 1 125(Octal) = 175 (Decimal)
4.2. Octal a Binario
4.2.1. Cada numero octal se convierte en su vinario equivalente a 3 bits y se juan en el mismo orden

