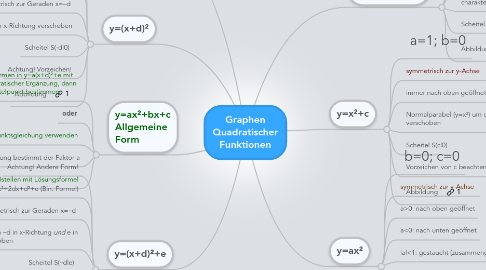
Graphen Quadratischer Funktionen
par Ivo Schwalbe

1. y=(x+d)²
1.1. Achtung! Andere Form!
1.2. y=x²+2dx+d² (Bin. Formel)
1.3. symmetrisch zur Geraden x=–d
1.4. Normalparabel um –d in x-Richtung verschoben
1.5. Scheitel S(-d|0)
1.6. Achtung! Vorzeichen!
1.7. Abbildung
2. y=(x+d)²+e
2.1. Achtung! Andere Form!
2.2. y=x²+2dx+d²+e (Bin. Formel)
2.3. symmetrisch zur Geraden x=–d
2.4. Normalparabel um –d in x-Richtung *und* e in y-Richtung verschoben
2.5. Scheitel S(–d|e)
2.6. Achtung! Vorzeichen!
2.7. Achtung! In machen Lehrbüchern trifft man auch die Form y=(x-d)²+e oder y=(x-x0)²+y0 an.
2.8. Abbildung
3. y=ax²+bx+c Allgemeine Form
3.1. Umformen in y=a(x+d)²+e mit quadratischer Ergänzung, dann Scheitelpunkt bestimmen
3.2. oder
3.3. Scheitelpunktsgleichung verwenden
3.4. Öffnung und Krümmung bestimmt der Faktor a
3.5. Nullstellen mit Lösungsformel
4. Allgemeines
4.1. Graph ist "Parabel"
4.2. Kegelschnitt
4.2.1. Gerade
4.2.2. Parabel
4.2.3. Hyperbel
4.2.4. Kreis
4.2.5. Ellipse
4.2.6. ...
