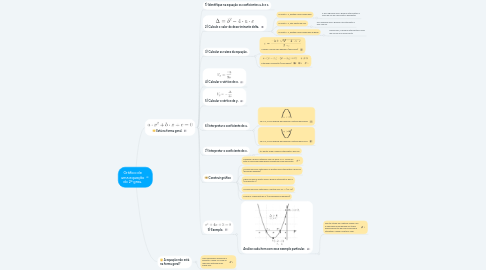
1. Está na forma geral.
1.1. 1) Identifique na equação os coeficientes a, b e c.
1.2. 2) Calcule o valor do descriminante delta.
1.2.1. Se Delta > 0, existem duas raízes reais.
1.2.1.1. E isso significa que o gráfico interceptará o Eixo real Ox em dois pontos diferentes.
1.2.2. Se Delta < 0, não existe raiz real.
1.2.2.1. Isso significa que o gráfico não intercepta o Eixo real Ox.
1.2.3. Se Delta = 0, existem duas raízes reais e iguais.
1.2.3.1. Nesse caso, o gráfico interceptará o Eixo real Ox em um único ponto.
1.3. 3) Calcular as raízes da equação.
1.3.1. Usando a fórmula da Bháskara (demorado)
1.3.2. Fatorando a equação (mais rápido)
1.4. 4) Calcular o vértice de x.
1.5. 5) Calcular o vértice de y.
1.6. 6) Interpretar o coeficiente de a.
1.6.1. Se a<0, a concavidade da parábola é voltada para baixo
1.6.2. Se a>0, a concavidade da parábola é voltada para cima.
1.7. 7) Interpretar o coeficiente de c.
1.7.1. É o ponto onde o gráfico intercepta o Eixo Oy.
1.8. 8) Construir gráfico
1.8.1. Desenhe o plano cartesiano com os eixos X e Y. Clique na seta ao lado para pegar papel milimetrado para impressão.
1.8.2. Localize no plano cartesiano os pontos que interceptam o Eixo Ox (Raízes da equação)
1.8.3. Agora localize o ponto onde o gráfico intercepta o Eixo y. (Coeficiente c)
1.8.4. Localize no plano cartesiano o vértice de x e y. V (Vx; Vy)
1.8.5. Analise o coeficiente de a. (Concavidade da parábola)
1.9. 9) Exemplo.
1.9.1. Analise cada item com esse exemplo particular.
1.9.1.1. Que tal utilizar um material criado com o GeoGebra onde poderá ver todos esses elementos de forma animada e interativa? Clique na seta ao lado.

