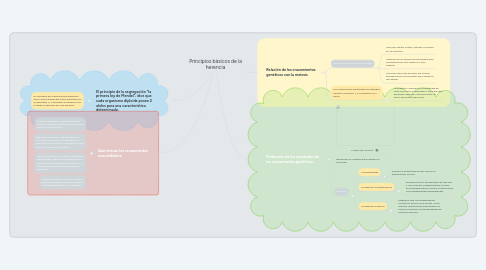
1. El principio de la segregación "la primera ley de Mendel", dice que cada organismo diploide posee 2 alelos para una característica determinada.
1.1. El concepto de la dominancia establece que 2 alelos diferentes están presentes en un genotipo y, el fenotipo se observa solo el rasgo codificado por uno de ellos.
2. Qué relevan los cruzamientos monohíbridos.
2.1. Primera conclusión: cada planta debe poseer 2 factores genéticos codificantes para una característica.
2.2. Segunda conclusión: Obtuvo que los 2 alelos de una planta se separaban en el momento de formarse los gametos y cada alelo iba a un gameto distinto.
2.3. Tercera conclusión: Mendel los denominó dominantes y resesivos; cuando un alelo dominante y un resesivo están juntos, el resesivo se encuentra enmascarado o suprimido.
2.4. Cuarta conclusión: dos alelos de una planta individual se separan con igual probabilidad dentro de los gametos.
3. Relación de los cruzamientos genéticos con la meiosis
3.1. Teoría cromosómica de la herencia
3.1.1. 1900 por Walter Sutton, estudió la meiosis en los insectos
3.1.2. Cada par de cromosomas homólogos está compuesta por uno materno y otro paterno.
3.1.3. Concluyó que este proceso era la base biológica para los principios de la herencia de Mandel.
3.2. Los cromosomas homólogos se segregan durante la anafase 1, y se separan los 2 alelos.
3.2.1. La anafase II separa los 2 cromátides de cada cromosoma duplicado y cada gameto generado durante la meiosis porta un único alelo para cada locus.
4. Predicción de los resultados de los cruzamientos genéticos.
4.1. Cuadro de Punnett
4.2. Desarrollar un método para predecir el resultado.
4.3. REGLAS
4.3.1. La probabilidad
4.3.1.1. expresa la posibilidad de que ocurra un determinado suceso.
4.3.2. La regla de la multiplicación
4.3.2.1. Establece que la probabilidad de que dos o más eventos independientes ocurran simultáneamente se calcula multiplicando sus probabilidades dependientes.
4.3.3. La regla de la adición
4.3.3.1. Establece que la probabilidad de ocurrencia de uno solo de dos o más eventos mutuamente excluyentes se calcula sumando las probabilidades de cada uno de ellos.
