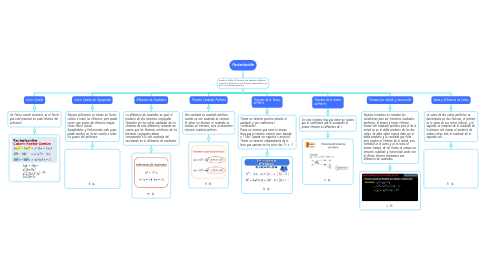
1. Cuando se habla de factorizar una expresión algebraica, consiste en hallar dos o más factores, cuyo producto sea igual a la expresión propuesta.
1.1. Factor Común
1.1.1. Un factor común monomio, es el factor que está presente en cada término del polinomio.
1.1.1.1. 4ab + 10ac= a(4b+10c) a(2*2b+2*5c) 2a(2b+5c
1.2. Factor Común por Agrupación
1.2.1. Algunos polinomios no tienen un factor común a todos los términos; pero puede ocurrir que grupos de términos tengan cierto factor común. Agrupándolos y factorizando cada grupo puede resultar un factor común a todos los grupos del polinomio.
1.2.1.1. k
1.3. Diferencia de Cuadrados
1.3.1. La diferencia de cuadrados es igual al producto de dos binomios conjugados formados por las raíces cuadradas de los términos de esta diferencia, teniendo en cuenta que los términos simétricos de los binomios conjugados deben corresponder a la raíz cuadrada del sustraendo en la diferencia de cuadrados.
1.3.1.1. m
1.4. Trinomio Cuadrado Perfecto
1.4.1. Una cantidad es cuadrado perfecto cuando su raíz cuadrada es racional. Al elevar un binomio al cuadrado se obtiene un trinomio, este se denomina trinomio cuadrad perfecto.
1.4.1.1. ñ
1.5. Trinomio de la forma: x2+bx+c
1.5.1. Tienen un termino positivo elevado al cuadrado y con coeficiente 1 (coeficiente). Posee un termino que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo). Tienen un termino independiente de la letra que aparece en los otros dos (+ o -).
1.5.1.1. b
1.6. Trinomio de la forma: ax2+bx+c
1.6.1. En este trinomio hay que tener en cuenta que el coeficiente que le acompaña al primer término es diferente de 1
1.6.1.1. n
1.7. Trinomio por adición y sustracción
1.7.1. Algunos trinomios no cumplen las condiciones para ser trinomios cuadrados perfectos, el primer y tercer término tienen raíz cuadrada perfecta pero el de la mitad no es el doble producto de las dos raíces. Se debe saber cuanto debe ser el doble producto y la cantidad que falte para cuadrar el término de la mitad, esta cantidad se le suma y se le resta al mismo tiempo, de tal forma se armara un trinomio cuadrado y factorizado unido con el último término tendremos una diferencia de cuadrados.
1.7.1.1. v
1.8. Suma y Diferencia de Cubos
1.8.1. La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone de el cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.
1.8.1.1. h
