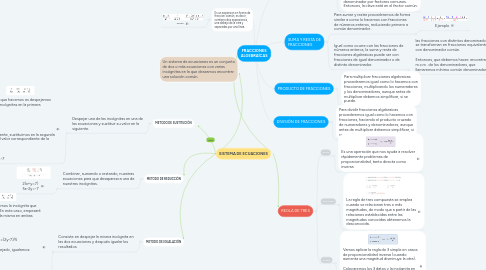
1. METODO DE IGUALACIÓN
1.1. Consiste en despejar la misma incógnita en las dos ecuaciones y después igualar los resultados.
1.1.1. En primer lugar, elegimos la incógnita que deseamos despejar. En este caso, empezaré por la «x» y despejo la misma en ambas ecuaciones. x+y=7; x=7-y 5x-2y=-7; 5x=2y-7; x=(2y-7)/5 Una vez hemos despejado, igualamos: 7-y=(2y-7)/5 5(7-y=(2y-7)/5) 35-5y=2y-7 42=7y y=42/7=6 y=6
2. METODO DE SUSTITUCIÓN
2.1. Despejar una de las incógnitas en una de las ecuaciones y sustituir su valor en la siguiente.
2.1.1. Lo primero que hacemos es despejamos una de las incógnitas en la primera ecuación. x+y=7 x= 7-y Posteriormente, sustituimos en la segunda ecuación el valor correspondiente de la «x». 5x-2y=-7 5.(7-y)-2y=-7
3. METODO DE REDUCCIÓN
3.1. Combinar, sumando o restando, nuestras ecuaciones para que desaparezca una de nuestras incógnitas.
3.1.1. 2(x+y=7) 5x-2y=-7
4. Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en la que deseamos encontrar una solución común.
5. Es un expresion en forma de fraccion común, es decir, contiene dos expresiones, una debajo de la otra y separadas por una línea.
5.1. Ejemplo
6. SISTEMA DE ECUACIONES
7. SIMPLIFICAR FRACCIONES
7.1. La simplificación de fracciones algebraicas es objeto de frecuentes errores, pero se simplifican igual que las fracciones ordinarias: dividiendo el numerador y el denominador por factores comunes. Entonces, la clave está en el factor común.
8. SUMA Y RESTA DE FRACCIONES
8.1. Para sumar y restar procederemos de forma similar a como lo hacemos con fracciones de números enteros, reduciendo primero a común denominador .
8.1.1. Ejemplo
8.2. Igual como ocurre con las fracciones de números enteros, la suma y resta de fracciones algebraicas puede ser con fracciones de igual denominador o de distinto denominador.
8.2.1. las fracciones con distintos denominadores se transforman en fracciones equivalentes con denominador común. Entonces, que debemos hacer: encontrar el m.c.m . de los denominadores, que llamaremos mínimo común denominador
8.2.1.1. Ejemplo
9. PRODUCTO DE FRACCIONES
9.1. Para multiplicar fracciones algebraicas procederemos igual como lo hacemos con fracciones, multiplicando los numeradores y los denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
10. DIVISIÓN DE FRACCIONES
10.1. Para dividir fracciones algebraicas procederemos igual como lo hacemos con fracciones, haciendo el producto cruzado de numeradores y denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
11. REGLA DE TRES
11.1. SIMPLE
11.1.1. Es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa.
11.2. COMPUESTA
11.2.1. La regla de tres compuesta se emplea cuando se relacionan tres o más magnitudes, de modo que a partir de las relaciones establecidas entre las magnitudes conocidas obtenemos la desconocida.
11.3. INVERSA
11.3.1. Vamos aplicar la regla de 3 simple en casos de proporcionalidad inversa (cuando aumenta una magnitud disminuye la otra). Colocaremos los 3 datos y la incógnita en la tabla igual que los hemos colocado en el caso anterior. Pero aplicaremos una fórmula distinta:
