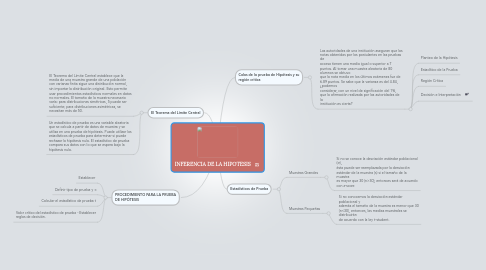
INFERENCIA DE LA HIPOTESIS

1. El Teorema del Límite Central

1.1. El Teorema del Límite Central establece que la media de una muestra grande de una población con varianza finita sigue una distribución normal, sin importar la distribución original. Esto permite usar procedimientos estadísticos normales en datos no normales. El tamaño de la muestra necesario varía: para distribuciones simétricas, 5 puede ser suficiente; para distribuciones asimétricas, se necesitan más de 50.

1.2. Un estadístico de prueba es una variable aleatoria que se calcula a partir de datos de muestra y se utiliza en una prueba de hipótesis. Puede utilizar los estadísticos de prueba para determinar si puede rechazar la hipótesis nula. El estadístico de prueba compara sus datos con lo que se espera bajo la hipótesis nula.

2. PROCEDIMIENTO PARA LA PRUEBA DE HIPÓTESIS

2.1. Establecer

2.2. Definir tipo de prueba y ∝

2.3. Calcular el estadístico de prueba t

2.4. Valor crítico del estadístico de prueba - Establecer reglas de decisión.

3. Colas de la prueba de Hipótesis y su región critica

3.1. Las autoridades de una institución aseguran que las notas obtenidas por los postulantes en las pruebas de acceso tienen una media igual o superior a 7 puntos. Al tomar una muestra aleatoria de 80 alumnos se obtuvo que la nota media en los últimos exámenes fue de 6.89 puntos. Se sabe que la varianza es del 4.84, ¿podemos considerar, con un nivel de significación del 1%, que la afirmación realizada por las autoridades de la institución es cierta?

3.1.1. Planteo de la Hipótesis

3.1.2. Estadítico de la Prueba

3.1.3. Región Crítica

3.1.4. Decisión e Interpretación

4. Estadísticos de Prueba

4.1. Muestras Grandes

4.1.1. Si no se conoce la desviación estándar poblacional (σ), ésta puede ser reemplazada por la desviación estándar de la muestra (s) si el tamaño de la muestra es mayor que 30 (n>30), entonces será de acuerdo con z-score

4.2. Muestras Pequeñas

4.2.1. Si no conocemos la desviación estándar poblacional y además el tamaño de la muestra es menor que 30 (n<30), entonces, las medias muestrales se distribuirán de acuerdo con la ley t-student.