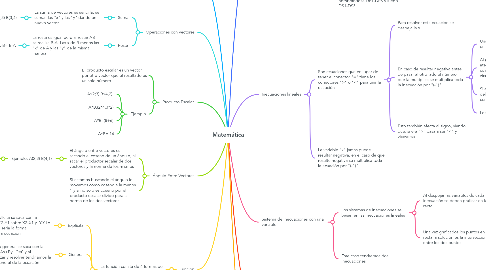
1. Vector unitario
1.1. El vector unitario, es aquel que tiene la misma dirección y sentido
1.1.1. Ejemplo: A(1,0)
1.1.1.1. Sacamos el módulo que sería
1.1.1.1.1. (1^2+0^2) Raíz
1.2. Su módulo debe ser igual a 1
1.3. Este vector se obtiene al dividir V por su módulo
2. Operaciones con vectores
2.1. Suma
2.1.1. La suma de vectores es sencilla, se suman las "x" y las "y" dando un nuevo vector
2.1.1.1. Ejemplo: A(2,3) B(3,4)
2.1.1.1.1. A+B: (2+3,3+4)
2.1.1.1.2. A+B: (5,7)
2.2. Resta
2.2.1. La resta es igual pero al restar AB se realiza B-A. Las x de B menos las "x" de A y las "y" de la misma manera
2.2.1.1. A-B= B-A
2.2.1.1.1. A-B: (3-2,4-3)
2.2.1.1.2. A-B: (1,1)
3. Producto Escalar
3.1. El producto escalar es un vector por otro vector que el resultado es un solo número
3.2. Ejemplo
3.2.1. A:(2;3) B:(4,2)
3.2.2. A*B:(2*4;3*2)
3.2.3. A*B: (8+6)
3.2.4. A*B= 14
4. Ángulo Entre Vectores
4.1. El ángulo entre vectores es sacando el coseno de un ángulo, al sacar el productor escalar de dos vectores y la norma de los mismos
4.1.1. Ejemplo: A(2,3) B(4,1)
4.1.1.1. θ≈42.01∘
4.2. Si estamos buscando el ángulo lo movemos como coseno a la menos 1 y si no solo es coseno por el producto escalar divido para la norma de los dos vectores .
5. Función
5.1. La función consta de 4 formas de expresar la ecuación
5.1.1. Explícita
5.1.1.1. La forma explícita se saca con la fórmula m=Y2-Y1 sobre X2-X1 y Y-Y1= m (X-X1) esa sería la forma explícita de la ecuación
5.1.1.1.1. Ejemplo: A(1,2) B(3,6)
5.1.2. General
5.1.2.1. La forma general se saca con la fórmula Ax+By+C=0 y al reemplazar y resolver tendríamos la forma general de la ecuación
5.1.2.1.1. Ejemplo: A(1,2) B(3,6)
5.1.3. Vectorial
5.1.3.1. La forma vectorial de la ecuación se saca con la fórmula X,Y= OA +k AB
5.1.3.1.1. Ejemplo: A(1,2) B(3,6)
5.1.4. Paramétrica
5.1.4.1. La forma paramétrica de la ecuación se saca al hacer un sistema de ecuaciones, y agregar la variable k usando la propiedad distributiva
5.1.4.1.1. Ejemplo: A(1,2) B(3,6)
6. Determinante por el método de Sarrus
6.1. Es un método para resolver sistema de ecuaciones de tres variables
6.1.1. Lo primero que se hace es alinear las ecuaciones para encontrar la determinante general
6.1.1.1. Para encontrar la determinante de "x" se debe colocar en lugar de x en las ecuaciones el número de los términos independientes
6.1.1.1.1. Al final cuando se tengan todas las determinantes se tiene que dividir la determinante de x sobre la determinante general y ese sería el resultado de la variable "x"
6.1.1.2. Hay que encontrar también la determinante de "y" y se repite el mismo proceso, se reemplaza "y" por los términos indepentientes y luego se multiplica en diagonal
6.1.1.2.1. Para conseguir la variable "y" se divide la determinante de y sobre la determinante general
6.1.1.3. Hay que econtrar la determinante de "z" y se repite, se reemplaza "z" por los términos indepentientes y luego se multiplica en diagonal
6.1.1.3.1. Para conseguir el valor de "z" se divide la determinante de z sobre la determinante general
6.1.2. Una vez que solo se pongan los números son tres filas, se repiten las dos primeras para llenar hasta tener 5
6.2. Se debe encontrar la determinante de cada variable
6.3. Al tener 5 filas se multiplica en diagonal tres veces hacia abajo y tres veces hacia arriba nombrándose DP1-DP3 y luego DS1-DS3
7. Inecuaciones lineales
7.1. Son ecuaciones que en lugar de tener el conector "=" tiene los conectores ">" o "<" para unir la ecuación
7.1.1. Para resolver esta ecuación se despeja la x
7.1.2. En caso de resultar negativa antes de pasar al otro lado el número que la multiplica se multiplica toda la inecuación por "(-1)"
7.1.2.1. Una vez despejada la x se grafica en una recta
7.1.2.2. Al graficar la recta se debe prestar atención al conector siendo que, si es mayor se va hacia la derecha y viceversa
7.1.2.2.1. Ejemplo: 3x−5≥7
7.1.2.3. Si el conector tiene un igual por debajo el corchete tiene que ir cerrado (incluye al número)
7.1.2.4. Los infinitos siempre son abiertos
7.1.3. Esto también afecta al signo, siendo que, si era ">" pasa a ser "<" y viceversa
7.2. La variable "x" jamás puede resultar negativa, en el caso de que resulte negativa se multiplica toda la ecuación por "(-1)"
8. Sistema de inecuaciones con una variable
8.1. Los sistemas de inecuaciones se basan en las inecuaciones lineales
8.1.1. Al despejar las variables de cada inecuación se deben graficar en la recta
8.1.1.1. Ejemplo
8.1.1.1.1. 2x−3>5 x+4≤10
8.1.2. Una vez graficados los puntos en la recta la solución es la intersección entre los dos puntos
8.2. Este caso tendremos dos inecuaciones
9. Inecuaciones con valor absoluto
9.1. Son ecuaciones que tienen dos partes
9.1.1. Si el signo es "<" se tiene que usar la fórmula -a < x < a
9.1.1.1. Ejemplo: ∣2x−3∣≤5
9.1.1.1.1. 2x−3≤5
9.1.1.1.2. −(2x−3)≤5
9.2. Lo que está antes de el conector se le denomina |x|
9.2.1. Una vez resueltas las operaciones deben darnos dos respuestas
9.2.1.1. Tenemos que graficar ambas respuestas en la recta y la solución es la intersección entre ellas
9.3. Lo que se encuentra después de el conector se le denomina "a"
9.3.1. Si el signo es ">" se debe usar la fórmula "x > a" o "x >-a"
9.3.1.1. Ejemplo: ∣2x−3∣>5
9.3.1.1.1. 2x−3>5
9.3.1.1.2. 2x−3<−5
9.3.2. De todas formas se deben usar ambas fórmulas
10. Módulo de vectores
10.1. Para encontrar el módulo de un vector se debe usar el teorema de Pitágoras
10.1.1. Ejemplo: A=(2;3)
10.1.2. Se eleva el 2 al cuadrado y el 3 al cuadrado
10.1.2.1. El resultado sería 4 + 9
10.1.2.2. Al sumarlos sería "13"
10.1.2.2.1. Se saca la raíz del número y ese sería el módulo
