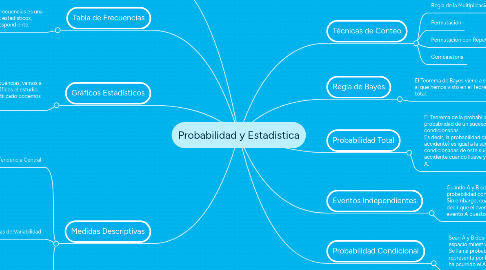
Probabilidad y Estadistica

1. Estadística Descriptiva

1.1. Registra los datos en tablas y los representa en gráficos. Calcula los parámetros estadísticos (medidas de centralización y de dispersión), que describen el conjunto estudiado.

2. Medidas Descriptivas

2.1. Medidas de Tendencia Central

2.1.1. Media

2.1.2. Mediana

2.1.3. Moda

2.2. Medidas de Variabilidad

2.2.1. La varianza Muestral

2.2.2. Mediana de las Desviaciones Absolutas (la media)

2.2.3. La Desviación Estándar Muestral

2.2.4. El Rango Intercuartilico

2.2.5. El Coeficiente de Variación

2.3. Medidas de Posición

2.3.1. Quartiles

2.3.2. Deciles

2.3.3. Percentiles

3. Técnicas de Conteo

3.1. Regla de la Multiplicación

3.2. Permutación

3.3. Permutación con Repeticiones

3.4. Combinatoria

4. Tabla de Frecuencias

4.1. La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.

4.1.1. Frecuencia Absoluta

4.1.2. Frecuencia Relativa

4.1.3. Frecuencia Acumulada

4.1.4. Frecuencia Relativa Acumulada

5. Gráficos Estadísticos

5.1. Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar:

5.1.1. Diagrama de Barras

5.1.2. Histograma

5.1.3. Polígono de Frecuencias

5.1.4. Diagrama de Sectores

6. Regla de Bayes

6.1. El Teorema de Bayes viene a seguir el proceso inverso al que hemos visto en el Teorema de la probabilidad total:

7. Probabilidad Total

7.1. El Teorema de la probabilidad total nos permite calcular la probabilidad de un suceso a partir de probabilidades condicionadas. Es decir, la probabilidad de que ocurra el suceso B (en nuestro ejemplo, que ocurra un accidente) es igual a la suma de multiplicar cada una de las probabilidades condicionadas de este suceso con los diferentes sucesos A (probabilidad de un accidente cuando llueve y cuando hace buen tiempo) por la probabilidad de cada suceso A.

8. Eventos Independientes

8.1. Cuando A y B son dos eventos con probabilidades positivas, hemos visto que en general la probabilidad condicional del evento B dado el evento A es diferente de la probabilidad del evento B. Sin embargo, cuando se tiene la igualdad: P(B/A) = P(B) es de especial importancia porque esto quiere decir que el evento B no depende o es independiente del evento A. Es decir, no importa si ocurrió o no el evento A puesto que la ocurrencia o no de A no afecta al evento B.

9. Probabilidad Condicional

9.1. Sean A y B dos sucesos de un mismo espacio muestral E. Se llama probabilidad del suceso B condicionado a A y se representa por P(B/A) a la probabilidad del suceso B una vez ha ocurrido el A.