1. Como preservan el producto interno se puede probar que también preservan la norma y las distancias
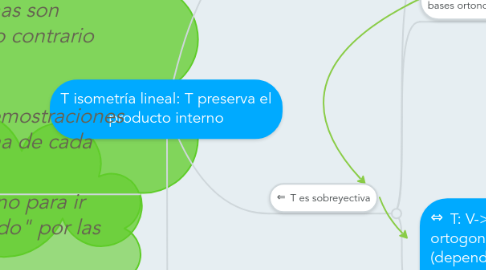
2. ⇐ T es sobreyectiva
2.1. ⇔las dimensiones del espacio de entrada y salida son iguales
2.2. ⇔Llevan bases ortonormales a bases ortonormales
2.3. ⇔ T: V->V es un operador ortogonal/unitario (T^-1=T*) (depende de si el cuerpo son los reales o los complejos)
2.3.1. ⇔ b(T)b=A es una matriz ortogonal/unitaria, donde B es una base ortonormal de V
2.3.1.1. ⇔ Las columnas forman una base ortonormal de Rn/Cn (dependiendo de si A es ortogonal o unitaria) (p.i. usual)
2.3.1.2. Si A es una matriz unitaria, existe P unitaria tal que D=conj(tras(P))AP es diagonal
2.3.1.3. Las raíces del polinomio característico tienen módulo 1
2.3.2. T es unitario (K=C)
2.3.2.1. λ es vap ⇒ |λ| = 1
2.3.2.1.1. Raíces características tienen módulo 1
2.3.2.2. Existe una b.o.n. de vectores propios (T es diagonalizable). Si agrego que los vaps tienen módulo 1 tengo un ⇔
2.3.2.3. λ1 y λ2 vaps diferentes ⇒ S_λ1 y S_λ2 son ortogonales
2.3.3. T es ortogonal (K=R)
2.3.3.1. λ es vap ⇒ λ = ±1
2.3.3.1.1. Raíces características tienen módulo 1
2.3.3.2. λ1 y λ2 vaps diferentes ⇒ S_λ1 y S_λ2 son ortogonales