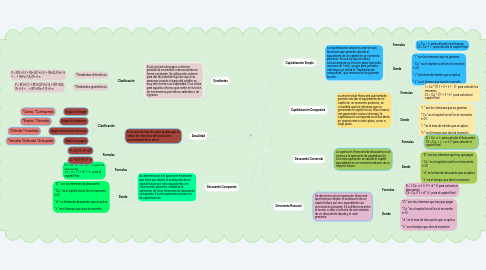
1. Descuento Compuesto
1.1. Se denomina así a la operación financiera que tiene por objeto la sustitución de un capital futuro por otro equivalente con vencimiento presente, mediante la aplicación de la ley financiera de descuento compuesto. Es una operación inversa a la de capitalización.
1.1.1. Formulas
1.1.1.1. D = Co * (1 - (1 + d) ^ -t ) para el descuento Cf = Co * ( 1 + d ) ^ -t para el capital final
1.1.2. Donde
1.1.2.1. " D " son los intereses de descuento " Co " es el capital inicial (en el momento t=0) " d " es la tasa de descuento que se aplica " t " es el tiempo que dura la inversión
2. Anualidad
2.1. Es la serie de flujo de cajas iguales que se realiza en intervalos de tiempos(no necesariamente en años)
2.1.1. Clasificaciòn
2.1.1.1. Según el tiempo
2.1.1.1.1. *Ciertas *Contingentes
2.1.1.2. Según los intereses
2.1.1.2.1. *Simples *Generales
2.1.1.3. Según el momento de inicio
2.1.1.3.1. *Diferidas *Inmediatas
2.1.1.4. Según los pagos
2.1.1.4.1. *Vencidas *Ordinadas *Anticipadas
2.1.2. Formulas
2.1.2.1. P= A[1-(1+i)^-t/i]
2.1.2.2. A= P[i/1-(1+I)^ -t
3. Gradientes
3.1. Es el conjunto de pagos o ahorros periódicos crecientes o decrecientes en forma constante. Se utiliza este sistema para dar facilidad de flujo de caja a las personas cuando el pago del crédito es muy alto frente a su capacidad. O se utiliza para aquellos ahorros que están en función de incrementos periódicos salariales o de ingresos.
3.1.1. Clasificación
3.1.1.1. *Gradientes Aritméticos
3.1.1.1.1. P = R(1+i)-1 + (R+L)(1+i)-2 + (R+2L)(1+i)-3 + ... + (R+(n-1)L)(1+i)-n
3.1.1.2. *Gradientes geométricos
3.1.1.2.1. P = R(1+i)-1 + R(1+G)(1+i)-2 + R(1+G)2 (1+i)-3 + ... + R(1+G)n-1 (1+i)-n
4. Capitalización Simple
4.1. La capitalización simple es una formula financiera que permite calcular el equivalente de un capital en un momento posterior. Es una ley que se utiliza exclusivamente en el corto plazo (periodos menores de 1 año), ya que para periodos más largos se utiliza la "Capitalización compuesta", que veremos en la siguiente lección.
4.1.1. Formulas
4.1.1.1. I = Co * i * t para calcular los intereses Cf= Co + I para calcular el capital final
4.1.2. Donde
4.1.2.1. " I " son los intereses que se generan " Co " es el capital inicial (en el momento t=0) " i " es la tasa de interés que se aplica " t " es el tiempo que dura la inversión
5. Capitalización Compuesta
5.1. es otra formula financiera que también permite calcular el equivalente de un capital en un momento posterior, se considera que los intereses que va generando el capital inicial, ellos mismos van generando nuevos intereses. la capitalización compuesta se utiliza tanto en operaciones a corto plazo, como a largo plazo.
5.1.1. Formulas
5.1.1.1. I = Co * ((( 1 + i) ^ t ) - 1 ) para calcular los intereses. Cf = Co * (( 1 + i) ^ t) para calcular el capital final
5.1.2. Donde
5.1.2.1. " I " son los intereses que se generan " Co " es el capital inicial (en el momento t=0) " i " es la tasa de interés que se aplica " t " es el tiempo que dura la inversión
6. Descuento Comercial
6.1. La operación financiera de descuento es la inversa a la operación de capitalización. Con esta operación se calcula el capital equivalente en un momento anterior de un importe futuro.
6.1.1. Formulas
6.1.1.1. D = Co * d * t para calcular el descuento Cf = Co * ( 1 - ( d * t )) para calcular el capital final
6.1.2. Donde
6.1.2.1. " D " son los intereses que hay que pagar " Co " es el capital inicial (en el momento t=0) " d " es la tasa de descuento que se aplica " t " es el tiempo que dura la inversión
7. Descuento Racional
7.1. Se denomina así a la operación financiera que tiene por objeto la sustitución de un capital futuro por otro equivalente con vencimiento presente. Es la diferencia entre el monto o valor a la fecha de vencimiento de un documento deuda y el valor presente.
7.1.1. Formulas
7.1.1.1. D = ( Co * d * t ) / (1 + d * t) para calcular el descuento. Cf= Co / (1 + d * t) para el capital final
7.1.2. Donde
7.1.2.1. " D " son los intereses que hay que pagar " Co " es el capital inicial (en el momento t=0) " d " es la tasa de descuento que se aplica " t " es el tiempo que dura la inversión
