1. Math1
1.1. 집합
1.1.1. 집합과 원소
1.1.1.1. 정의
1.1.1.2. 집합과 원소, 집합과 집합 사이 관계
1.1.2. 분류
1.1.2.1. 유한집합
1.1.2.2. 무한집합
1.1.2.3. 공집합(유한집합)
1.1.3. 원소의 개수
1.1.3.1. n(Ø) = 0
1.1.3.2. n({Ø}) = 1
1.1.3.3. n({0}) = 1
1.1.3.4. n(0) : 틀린 표현
1.1.4. 집합의 표현 방법
1.1.4.1. 원소나열법
1.1.4.2. 조건제시법
1.1.4.3. 벤 다이어그램(비교에 유용)
1.1.5. 부분집합
1.1.5.1. 부분집합 성질
1.1.5.1.1. A ⊂ A
1.1.5.1.2. ∅ ⊂ A
1.1.5.1.3. A ∩ X = X ⇔ X ⊂ A
1.1.5.1.4. A ∪ X = X ⇔ A ⊂ X
1.1.5.2. 진부분집합
1.1.5.3. 부분집합 개수
1.1.5.3.1. 2^n
1.1.5.3.2. 2^(n-m)
1.1.6. 집합 연산
1.1.6.1. A ∪ B
1.1.6.2. A ∩ B
1.1.6.3. 여집합(보집합)
1.1.6.4. A - B
1.1.6.5. 교집합과 합집합 성질
1.1.6.5.1. A ∩ ∅
1.1.6.5.2. A ∪ ∅
1.1.6.5.3. (A ∩ B) ⊂ A ⊂ (A ∪ B)
1.1.6.6. 여집합과 차집합 성질
1.1.6.6.1. A - B = A ∩ B^c
1.1.6.7. 원소 갯수 관계식
1.1.6.7.1. n(A∪B) = n(A) + n(B) - n(A ∩ B)
1.1.6.7.2. n(A - B) = n(A) - n(A ∩ B)
1.1.6.7.3. n(A - B) = n(A∪B) - n(B)
1.1.6.7.4. 벤 그림에서 분할된 각 영역에 문자(a,b,c,d,...)를 넣고 식을 만들자
1.2. 수
1.2.1. R(실수)
1.2.1.1. Q(유리수)
1.2.1.1.1. Z(정수)
1.2.1.1.2. 정수가 아닌 유리수
1.2.1.2. I(무리수)
1.2.1.2.1. 순환하지 않는 무한 소수
1.2.2. 수의 대소
1.2.2.1. 수직선과 절대값
1.2.2.2. 이상,이하,이내
1.2.2.3. R,I,Q,Z,N 사이의 포함관계
1.2.3. 수의 사칙연산
1.2.3.1. 덧셈,곱셈의 교환법칙
1.2.3.2. 덧셈,곱셈의 결합법칙
1.2.3.3. 역수
1.2.3.4. 분배법칙
1.2.3.5. 혼합식의 계산순서
1.2.4. 자연수
1.2.4.1. 소인수 분해
1.2.4.1.1. 약수
1.2.4.1.2. 약수의 개수,합
1.2.4.1.3. GCD
1.2.4.1.4. LCM
1.2.4.1.5. GCD와 LCM 성질
1.2.4.1.6. 제곱수
1.2.4.1.7. 분수 ⇒ 자연수
1.2.4.2. 서로소 (ex. 4,9)
1.3. 기수법
1.3.1. 수와 숫자
1.3.2. 위치적 기수법
1.3.3. 전개식
1.3.4. 십진법
1.3.5. 이진법
1.3.5.1. 2진법 덧셈과 뺄셈
1.3.6. 진법 변환
1.4. 문자식
1.4.1. 용어
1.4.1.1. 항
1.4.1.1.1. 단항
1.4.1.1.2. 다항
1.4.1.2. 계수
1.4.1.3. 차수
1.4.1.3.1. 일차
1.4.1.3.2. 이차
1.4.1.4. 상수항
1.4.2. 다항식의 덧셈과 뺄셈
1.4.2.1. 동류항
1.4.2.2. 분배법칙
1.4.2.2.1. 풀기
1.4.2.2.2. 묶기
1.4.3. 식
1.4.3.1. 등식
1.4.3.1.1. 등호,좌변,우변,양변
1.4.3.1.2. 방정식
1.4.3.1.3. 항등식
1.4.3.1.4. 등식 성질
1.4.3.2. 부등식
1.4.4. 속력
1.4.4.1. 속력 = 거리 / 시간 (km/h)
1.4.4.2. 시간 = 거리 / 속력
1.4.5. 농도
1.4.5.1. 농도 = 용질 / 용액 × 100 (%)
1.4.5.2. 용질 = 용액 × 비율
1.4.5.3. 용액 = 용질 + 용매
1.5. 함수
1.5.1. 비례식(관계식)
1.5.1.1. 정비례
1.5.1.1.1. y = ax
1.5.1.1.2. y / x = a ; 비가 일정
1.5.1.2. 반비례
1.5.1.2.1. y = a / x
1.5.1.2.2. y x = a ; 곱이 일정
1.5.2. 개념
1.5.2.1. 함수의 정의
1.5.2.2. 정의역,공역,치역
1.5.2.3. 함수값
1.5.2.4. 변수,상수
1.5.3. 좌표
1.5.3.1. 좌표평면(x축,y축,원점,순서쌍,사분면)
1.5.3.2. 대칭(x, y, 원점)
1.5.4. 그래프
1.5.4.1. y = ax
1.5.4.1.1. a ≠ 0
1.5.4.1.2. a > 0
1.5.4.1.3. a < 0
1.5.4.1.4. a의 절대값이 클수록 y축에 가깝다
1.5.4.2. y = a / x
1.5.4.2.1. a ≠ 0 && x ≠ 0
1.5.4.2.2. a > 0
1.5.4.2.3. a < 0
1.5.4.2.4. a의 절대값이 클수록 원점에서 멀어진다
1.5.4.2.5. 원점과 곡선위의 임의의 점으로 만들어지는 직사각형의 넓이는 a의 절대값이다
1.5.4.3. 함수의 관계식 ⇔ 그래프
1.5.5. 방정식 vs 관계식
1.5.5.1. 방정식에서는 미지수를 구한다
1.5.5.2. 관계식에서는 변수의 쌍을 구한다
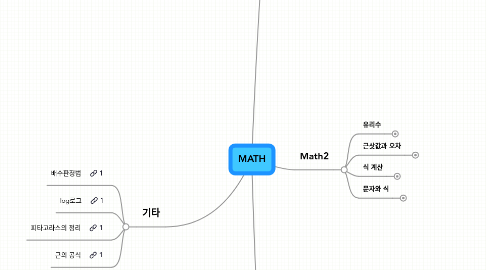
2. Math2
2.1. 유리수
2.1.1. 정의
2.1.2. 분수와 유한소수
2.1.2.1. 분수 → 유한소수
2.1.2.1.1. 기약분수 분모의 소인수가 2,5뿐인 분수
2.1.2.1.2. 분모를 소인수분해해서 10의 거듭제곱으로 만들고
2.1.2.1.3. 유한소수 값으로
2.1.2.2. 유한소수 → 분수
2.1.2.2.1. 분모가 10의 거듭제곱인 분수로 만들고
2.1.2.2.2. 약분
2.1.3. 순환소수
2.1.3.1. 기약분수 분모의 소수가 2,5 이외의수를 갖는 분수
2.1.3.2. 분수표현
2.1.3.2.1. 순환소수를 x로 놓고
2.1.3.2.2. 순환마디가 일치하도록 10의 거듭제곱을 곱해
2.1.3.2.3. 분수를 구해 기약분수로 표현
2.1.3.3. 대소 비교
2.1.3.3.1. 9가 순환하는 소수는 꼭 분수로 바꿔 비교
2.2. 근삿값과 오차
2.2.1. 참값
2.2.2. 측정값
2.2.3. 근삿값
2.2.3.1. 측정값
2.2.3.2. 반올림값
2.2.4. 참값 범위
2.2.4.1. 오차
2.2.4.1.1. 근삿값 - 참값
2.2.4.1.2. 오차 한계 (반올림 한계)
2.2.4.2. 근삿값 - 오차한계 ≤ 참값 < 근삿값 + 오차한계
2.2.5. 근삿값 표현
2.2.5.1. 유효숫자
2.2.5.1.1. *근삿값*에서 반올림 하지 않은 부분의 숫자
2.2.5.1.2. 측정 장비 *최소 눈금* 숫자부터
2.2.5.1.3. 유효숫자 판별
2.2.5.2. 유효숫자(정수가 한자리인 소수) × 10의 거듭제곱
2.2.5.2.1. 4500 ; 유효숫자 판별 불가능
2.2.5.2.2. 4500 → 4.50 × 10^3 ; 유효 숫자 => 4,5,0
2.2.5.2.3. 0.00230 → 2.30 × 10^-3
2.2.6. 근삿값의 덧셈,뺄셈
2.2.6.1. 계산후
2.2.6.2. 오차의 한계가 큰 수의 끝자리에 맞추어 반올림한다
2.2.6.2.1. 오차의 한계가 큰수 => 부정확한 근삿값
2.3. 식 계산
2.3.1. 지수법칙
2.3.1.1. a^m × a^n = a^(m+n)
2.3.1.2. a^m ÷ a^n = a^(m-n)
2.3.1.3. (a^m)^n = a^(m×n)
2.3.1.4. (ab)^m = a^m × b^m
2.3.2. 단항식
2.3.2.1. 계산
2.3.2.1.1. 계수는 계수끼리, 문자는 문자끼리
2.3.2.1.2. 지수법칙 이용!
2.3.2.1.3. 나눗셈은 역수(분수의 곱셈)로 바꿔 계산
2.3.3. 다항식
2.3.3.1. 덧셈,뺄셈
2.3.3.1.1. 동류항 정리
2.3.3.2. 곱셈,나눗셈
2.3.3.2.1. 분배법칙
2.3.3.2.2. 나눗셈은 역수의 곱셈
2.4. 문자와 식
2.4.1. 방정식
2.4.1.1. 미지수가 2(x,y)개인
2.4.1.1.1. 일차방정식
2.4.1.1.2. 연립일차방정식
2.4.2. 부등식
2.4.2.1. 부등호
2.4.2.1.1. > (초과)
2.4.2.1.2. < (미만)
2.4.2.1.3. ≥ (이상)
2.4.2.1.4. ≤ (이하)
2.4.2.2. 부등식 성질
2.4.2.2.1. 음수를 곱하거나 나누면 부등호가 바뀐다
3. Math3
3.1. 제곱근과 실수
3.1.1. 제곱근
3.1.1.1. 넓이가 a인 정사각형의 한변의 길이 → √a
3.1.2. 제곱근의 개수
3.1.2.1. x > 0, 2개(양의 제곱근, 음의 제곱근)
3.1.2.2. x = 0, 1개(0)
3.1.2.3. x < 0, 0개
3.1.3. 제곱근 표현
3.1.3.1. 3의 제곱근 ; +√3, -√3
3.1.3.2. root 3 ; √3
3.1.3.3. 제곱근 3 ; √3
3.1.4. 제곱수
3.1.4.1. 11^2=121, 12^2=144, 13^2=169
3.1.4.2. 14^2=196, 15^2=225, 16^2=256
3.1.5. 제곱근의 성질
3.1.5.1. (√a)^2 = (-√a)^2 = a
3.1.5.2. √(a)^2 = 절대값 a
3.1.6. 무리수
3.1.6.1. 순환하지 않는 무한소수
3.1.6.2. 소수
3.1.6.2.1. 유한소수
3.1.6.2.2. 무한소수
3.1.7. √a의 정수부분과 소수부분
3.1.7.1. a를 포함하는 연속하는 두 제곱수를 찾아
3.1.7.2. 정수부분 결정
3.1.7.3. 소수부분 = 수 - 정수부분
3.1.8. 제곱근의 사칙연산
3.1.8.1. √a√b = √ab
3.1.8.2. √a / √b = √a/b
3.1.8.3. 분모의 유리화
3.1.8.3.1. √a / √b = √ab / b
3.1.8.4. m√a ± n√a = (m±n)√a (동류항)
3.1.8.5. √a(√b ± √c) = √ab ± √ac (분배법칙)
3.1.9. 근삿값
3.2. 일차방정식
3.2.1. 다항식의 곱셈 (전개)
3.2.1.1. 전개,전개식
3.2.1.1.1. 분배법칙
3.2.1.2. 곱셈공식
3.2.1.2.1. 완전제곱식
3.2.1.2.2. (ax+b)(cx+d) = acx^2 + (ad+bc)x + bd
3.2.2. 인수분해 (전개 역)
3.2.2.1. 인수
3.2.2.1.1. 인수분해 했을때, 곱을 구성하는 각각의 수나 식
3.2.2.2. vs. 소인수 분해
3.2.2.2.1. 소인수분해
3.2.2.2.2. 인수분해
3.2.2.3. 인수분해 공식
3.2.2.3.1. 분배법칙(공통인수)
3.2.2.3.2. 곱셈공식 역
