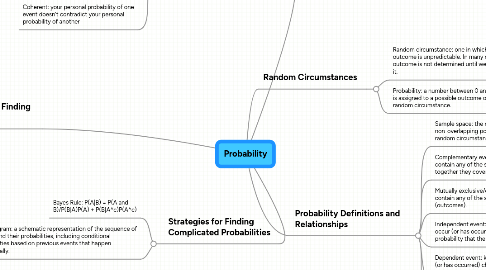
Probability
por Chelsea Gray

1. Interpretations of Probability
1.1. Relative frequency: In situations that we can imagine repeating many times, we define the probability of a specific out come as the proportion of times it would occur over the long run.
1.2. Personal probability: the degree to which a given individual believes that the event will happen
1.3. Subjective probability: The degree of belief may be different for each individual
1.4. Coherent: your personal probability of one event doesn't contradict your personal probability of another
2. Basic Rules for Finding Probabilities
2.1. Rule 1 ( "not the event"): to find the probability of A^c, the complement of A, use P(A^c) = 1 - P(A). P(A^c) is the probability that event A won't occur
2.2. Rule 2 (addition rule for "either/or"): to find the probability that either A or B or both happen.
2.2.1. Rule 2a (general): P(A or B) = P(A and B)
2.2.2. Rule 2b (for mutually exclusive events): if A and B are mutually exclusive events, P(A or B) = P(A) + P(B)
2.3. Rule 3 (multiplication rule for "and"): to find the probability that two events A and B both occur simultaneously or in a sequence.
2.3.1. Rule 3a (general): P(A and B) = P(A)P(B|A) = P(B)P(A|B)
2.3.2. Rule 3b (for independent events): if A and B are independent events, P(A and B) = P(A)P(B)
2.4. Rule 4 (conditional probability): an algebraic restatement of rule 3a
2.4.1. P(B|A) = P(A and B)/P(A)
2.5. Sample with replacement: individuals are returned to the eligible pool for each selection.
2.6. Sample without replacement: individuals are not eligible for subsequent selection.
3. Strategies for Finding Complicated Probabilities
3.1. Bayes Rule: P(A|B) = P(A and B)/P(B|A)P(A) + P(B|A^c)P(A^c)
3.2. Tree diagram: a schematic representation of the sequence of events and their probabilities, including conditional probabilities based on previous events that happen sequentially.
4. Random Circumstances
4.1. Random circumstance: one in which the outcome is unpredictable. In many cases the outcome is not determined until we observe it.
4.2. Probability: a number between 0 and 1 that is assigned to a possible outcome of a random circumstance.
5. Probability Definitions and Relationships
5.1. Sample space: the collection of unique, non-overlapping possible outcomes of a random circumstance.
5.1.1. Simple Event: one outcome in the sample space. Simple event is a possible outcome of a random circumstance.
5.1.1.1. Event: a collection of one or more simple events in the sample space. Often written using capital letters.
