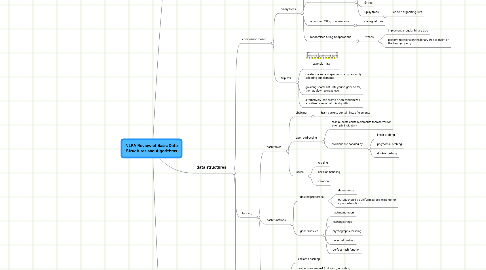
1. language classes
1.1. by machine
1.1.1. finite state automata
1.1.2. pushdown automata
1.1.3. linear bounded automata
1.1.4. turing machines
1.2. by language
1.2.1. regular
1.2.2. context free
1.2.3. context sensitive
1.2.4. phrase structure
1.2.5. (uncomputable)
1.3. by algorithm
1.3.1. recursive descent parsing
1.3.1.1. top-down parser
1.3.1.2. predictive
1.3.1.2.1. no backtracking
1.3.1.2.2. LL(k) grammars
1.3.1.2.3. context free, only examines next k tokens
1.3.1.2.4. no left recursion
1.3.1.3. backup
1.3.1.3.1. backtracking
1.3.1.3.2. may not terminate at all
1.3.1.3.3. may take exponential time
1.3.2. LR parsers
1.3.2.1. bottom-up parsers
1.3.2.2. deterministic context free languages
1.3.2.3. linear time
2. data structures
2.1. comparison-based
2.1.1. binary trees
2.1.1.1. unbalanced binary trees
2.1.1.2. worst case O(log n) operations
2.1.1.2.1. red-black trees
2.1.1.2.2. AVL trees
2.1.1.2.3. B-tree
2.1.1.2.4. Splay trees
2.1.1.3. amortized O(log n) operations
2.1.1.3.1. scapegoat tree
2.1.1.4. randomized O(log n) operations
2.1.1.4.1. treaps
2.1.2. skiplists
2.1.2.1. example
2.1.2.2. create sparser and sparser lists by randomly selecting subelements
2.1.2.3. go along sparse list until you've gone to far, then go down to next level
2.1.2.4. alternatively, can create a non-randomized, amortized version of this algorithm
2.2. hashing
2.2.1. hash tables
2.2.1.1. chaining
2.2.1.1.1. hash buckets contain lists of elements
2.2.1.2. open addressing
2.2.1.2.1. hash buckets contain elements themselves (or an empty indicator)
2.2.1.2.2. collisions are handled by
2.2.1.3. issues
2.2.1.3.1. resizing
2.2.1.3.2. collision handling
2.2.1.3.3. iteration
2.2.2. hash functions
2.2.2.1. desired properties
2.2.2.1.1. deterministic
2.2.2.1.2. output should be uniform across its range for input distributions
2.2.2.2. general issues
2.2.2.2.1. hashing numbers
2.2.2.2.2. hashing strings
2.2.2.2.3. cryptographic hashing
2.2.2.2.4. universal hashing
2.2.2.2.5. perfect hash function
2.2.3. Bloom filters
2.2.3.1. similar to hashing
2.2.3.2. hash entries are just 1 bit each, indicating whether that bucket has ever been used
2.2.3.3. if the Bloom filter returns false, the key has not been previously added
2.2.3.4. if the Bloom filter returns true, the key may have been added, or we may have a false positive
2.2.3.5. repeat with multiple bits to get probability estimates for false positives
2.3. alphabet-based
2.3.1. tries
2.3.2. radix tree
2.3.3. patricia tree
2.3.4. suffix tree
2.3.5. suffix array
3. algorithms
3.1. sorting
3.1.1. quicksort
3.1.2. mergesort
3.1.3. radix sort
3.2. Boyer-Moore
3.2.1. string search
3.2.2. UNIX tool: fgrep
3.2.3. problem
3.2.3.1. find a string in a text (perhaps repeatedly)
3.2.3.2. input: query, text, output: position of first match
3.2.3.3. can spend time and memory on preprocessing the string
3.2.3.4. preprocesses query, not text
3.2.4. brute force solution
3.2.4.1. match at position 0
3.2.4.2. return if match
3.2.4.3. advance to next position and repeat
3.2.5. Boyer-Moore
3.2.5.1. idea: when we look at one character in the text, it gives us additional information about positions where the string can't match
3.2.6. NB: you don't need to know the details of the algorithm, but you should know the name, what it does, and what the idea is
3.3. Hunt-McIlroy
3.3.1. longest common subsequence
3.3.2. UNIX tool: diff
3.3.3. problem
3.3.3.1. given two sequences, find the longest common subsequence (not substring)
3.3.4. NB: you don't need to know the details of the algorithm, but you should know the name and what it does
3.4. Levenshtein distance
3.4.1. minimum number of edits necessary to transform one string into another
3.4.2. UNIX tool: agrep
3.4.3. problem: given two input string, find the minimum number of insertions, deletions, and substitutions to transform one into another
3.4.4. solution: dynamic programming
3.4.5. (already covered this in previous classes; you need to know this algorithm well, it's the prototypical dynamic programming algorithm)
