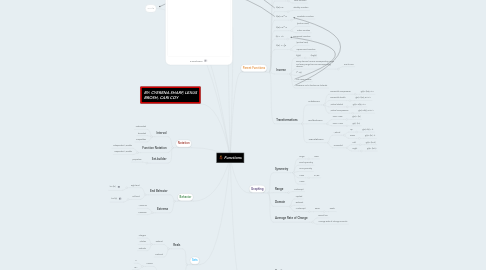
1. Functions
2. Sets
2.1. Reals
2.1.1. Rational
2.1.1.1. Integers
2.1.1.2. Wholes
2.1.1.3. Naturals
2.1.2. Irrational
2.2. Universal set
2.2.1. Unions
2.2.1.1. U
2.2.1.2. "or"
2.2.2. Intersections
2.2.2.1. "and"
2.2.2.2. ∩
2.2.3. Empty Set
3. Notation
3.1. Interval
3.1.1. Unbounded
3.1.2. bounded
3.1.3. inequalities
3.2. Function Notation
3.2.1. Independent Variable
3.2.2. Dependent Variable
3.3. Set-builder
3.3.1. properties
4. Behavior
4.1. End Behavior
4.1.1. Right End
4.1.1.1. lim f(x)
4.1.2. Left End
4.1.2.1. lim f(x)
4.2. Extrema
4.2.1. Minimum
4.2.2. Maximum
5. BY: CYERENA SHARP, LEXUS BROSH, CARI COY
6. <----
7. ----->
8. ----->
9. Graphing
9.1. Symmetry
9.1.1. Origin
9.1.1.1. ODD
9.1.2. Point Symmetry
9.1.3. Line Symmetry
9.1.4. Y-axis
9.1.4.1. EVEN
9.1.5. X-axis
9.2. Range
9.2.1. Y-intercept
9.3. Domain
9.3.1. Implied
9.3.2. Relevent
9.3.3. X-intercept
9.3.3.1. Zeros
9.3.3.1.1. Roots
9.4. Average Rate of Change
9.4.1. Secant line
9.4.2. Average Rate of Change Formula
10. Continuity Test
10.1. Continuous
10.1.1. Limit
10.2. Discontinuous
10.2.1. Removable
10.2.2. Nonremovable
10.2.2.1. Jump
10.2.2.2. Infinite
11. Parent Functions
11.1. f(x)=/x/
11.1.1. Absolute Value
11.2. f(x)=C
11.2.1. Constant Function
11.2.2. Zero Function
11.3. f(x)=x
11.3.1. Identity Function
11.4. f(x)=x^2
11.4.1. Quadratic Function
11.5. f(x)=x^3
11.5.1. (picture Here)
11.5.2. Cubic Function
11.6. f(x) = 1/x
11.6.1. Reciprocal Function
11.7. f(x) = √x
11.7.1. (picture here)
11.7.2. Square Root Function
11.8. Inverse
11.8.1. f(g(x))
11.8.1.1. (fog)(x)
11.8.2. Every domain has one corresponding range and every range has one corresponding domain.
11.8.2.1. one to one
11.8.3. f^-1(x)
11.8.4. Is It's own inverse
11.8.5. Inverse is not a function as it stands.
11.9. Transformations
11.9.1. Dilations
11.9.1.1. Horizontal Compression
11.9.1.1.1. g(x)= f(ax); a>1
11.9.1.2. Horizontal Stretch
11.9.1.2.1. g(x)= f(ax); 0<a<1
11.9.1.3. Vertical Stretch
11.9.1.3.1. g(x)= af(x); a>1
11.9.1.4. Vertical Compression
11.9.1.4.1. g(x)= af(x); 0<a<1
11.9.2. Reflections
11.9.2.1. Over Y-axis
11.9.2.1.1. g(x)= -f(x)
11.9.2.2. Over X-axis
11.9.2.2.1. g(x)- f(-x)
11.9.3. Translations
11.9.3.1. Vertical
11.9.3.1.1. Up
11.9.3.1.2. Down
11.9.3.2. Horizontal
11.9.3.2.1. Left
11.9.3.2.2. Right
