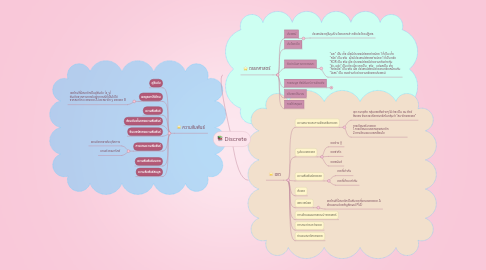
1. ความสัมพันธ์
1.1. คู่อันดับ
1.2. ผลคูรคาร์ทีเชียน
1.2.1. เซตใหม่ที่มีสมาชิกเป็นคู่อันดับ (x, y) อันเกิดจากการการจับคู่ทุกกรณีที่เป็นไปได้ จากสมาชิก x ของเซต A และสมาชิก y ของเซต B
1.3. ความสัมพันธ์
1.4. ส่วนเติมเต็มของความสัมพันธ์
1.5. อินเวอร์สของความสัมพันธ์
1.6. การแทนความสัมพันธ์
1.6.1. แทนด้วยกราฟระบุทิศทาง
1.6.2. แทนด้วยเมทริกซ์
1.7. ความสัมพันธ์บนเซต
1.8. ความสัมพันธ์สมมูล
2. ตรรกศาสตร์
2.1. ประพจน์
2.1.1. ประพจน์จะอยู่ในรูปประโยคบอกเล่า หรือประโยคปฏิเสธ
2.2. ประโยคเปิด
2.3. ตัวดำเนินการทางตรรกะ
2.3.1. “และ” เป็น เท็จ เมื่อมีประพจน์ย่อยอย่างน้อย 1 ที่เป็น เท็จ “หรือ” เป็น จริง เมื่อมีประพจน์ย่อยอย่างน้อย 1 ที่เป็น จริง “XOR เป็น จริง เมื่อ ประพจน์ย่อยมีค่าความจริงต่างกัน “ถ้า...แล้ว” เป็น เท็จ เมื่อ เหตุเป็น จริง แต่ผลเป็น เท็จ “ก็ต่อเมื่อ” เป็น จริง เมื่อ ประพจน์ย่อยมีค่าความจริงเหมือนกัน “นิเสธ” เป็น ตรงข้ามกับค่าความจริงของประพจน์
2.4. การสมมูล สัจนิรันดร์ การขัดแย้ง
2.4.1. เป็นรูปแบบของประพจน์ที่มีค่าความจริงเป็นจริงทุกกรณี
2.5. วลีบอกปริมาณ
2.6. การให้เหตุผล
3. เซต
3.1. ความหมายและการเขียนอธิบายเซต
3.1.1. เซต หมายถึง กลุ่มของสิ่งต่างๆ ไม่ว่าจะเป็น คน สัตว์ สิ่งของ ซึ่งเราจะเรียกสมาชิกในกลุ่มว่า “สมาชิกของเซต”
3.1.2. การเขียนอธิบายเซต 1.การเขียนแบบแจกแจงสมาชิก 2.การเขียนแบบบอกเงื่อนไข
3.2. รูปแบบของเซต
3.2.1. เซตว่าง {}
3.2.2. เซตจำกัด
3.2.3. เซตอนันต์
3.3. ความสัมพันธ์ของเซต
3.3.1. เซตที่เท่ากัน
3.3.2. เซตที่เทียบเท่ากัน
3.4. สับเซต
3.5. เพาเวอร์เซต
3.5.1. เซตใหม่ที่มีสมาชิกเป็นสับเซตทั้งหมดของเซต A เขียนแทนด้วยสัญลักษณ์ P(A)

