Funcţia de gradul II
oprea zenovieにより
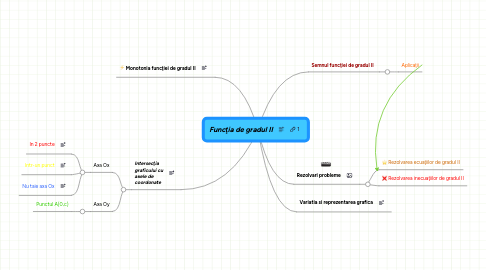

1. Intersecţia graficului cu axele de coordonate
1.1. Axa Ox
1.1.1. In 2 puncte
1.1.2. Intr-un punct
1.1.3. Nu taie axa Ox
1.2. Axa Oy
1.2.1. Punctul A(0,c)

1.1.1. In 2 puncte
1.1.2. Intr-un punct
1.1.3. Nu taie axa Ox
1.2.1. Punctul A(0,c)