Xposition.PositionDeltaSharpe = dPortfolioSharpe - Xposition.PositionSharpe;

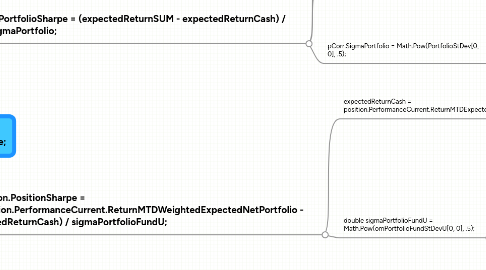
1. double dPortfolioSharpe = (expectedReturnSUM - expectedReturnCash) / pCorr.SigmaPortfolio;

1.1. double expectedReturnSUM += position.PerformanceCurrent.ReturnMTDExpectedNetPortfolio * position.PortfolioModelWeight;

1.2. double expectedReturnCash = position.PerformanceCurrent.ReturnMTDExpectedNetPortfolio;

1.3. pCorr.SigmaPortfolio = Math.Pow(PortfolioStDev[0, 0], .5);

1.3.1. Matrix PortfolioStDev = FundActualWeightTransposedMatrix * (RiskAdjustedCorrelation * FundActualWeightMatrix);

1.3.1.1. FundActualWeightMatrix = new Matrix(FundActualWeights, FundActualWeights.Length);

1.3.1.1.1. FundActualWeights[x] = position.PortfolioWeight;

1.3.1.2. Matrix FundActualWeightTransposedMatrix = new Matrix(FundActualWeights, FundActualWeights.Length); FundActualWeightTransposedMatrix.Transpose();

1.3.1.3. Matrix RiskAdjustedCorrelation = Matrix.MultipleRowColumn(Matrix.MultipleRowColumn(CorrelationMatrix, FundStDev, 1), FundStDev, 2);

1.3.1.3.1. CorrelationMatrix = corelation between returns; _returnsMatrix[x, y] = perf.ReturnMTDEstimateOrActualNetPortfolio x - position y - date

1.3.1.3.2. FundStDev, fundStDev[x] = double.IsNaN(stDevAnnualized) ? 0 : stDevAnnualized;

2. Xposition.PositionSharpe = (Xposition.PerformanceCurrent.ReturnMTDWeightedExpectedNetPortfolio - expectedReturnCash) / sigmaPortfolioFundU;

2.1. expectedReturnCash = position.PerformanceCurrent.ReturnMTDExpectedNetPortfolio;

2.2. double sigmaPortfolioFundU = Math.Pow(omPortfolioFundStDevU[0, 0], .5);

2.2.1. double sigmaPortfolioFundU = Math.Pow(omPortfolioFundStDevU[0, 0], .5);

2.2.1.1. Matrix omPortfolioFundStDevU = omFWUT * (pCorr.RiskAdjustedCorrelation * omFWU);

2.2.1.1.1. Matrix omFWU = new Matrix(dFundWeightsUp, dFundWeightsUp.Length);

2.2.1.1.2. Matrix omFWUT = Matrix.Transpose(omFWU);

2.2.1.1.3. Matrix RiskAdjustedCorrelation = Matrix.MultipleRowColumn(Matrix.MultipleRowColumn(CorrelationMatrix, FundStDev, 1), FundStDev, 2);